Production Function and Its Aspects (With Diagram)

The below mentioned article provides an overview on the Production Function and Its Aspects. After reading this article you will learn about: 1. The Production Function 2. The Law of Variable Proportions 3. The Law of Returns to Scale.

The Production Function:

The production function expresses a functional relationship between quantities of inputs and outputs it shows how and to what extent output changes with variations in inputs during a specified period of time. In the words of Stigler, The production function is the name given to the relationship between rates of input of productive services and the rate of output of product.

It is the economist’s summary of technical knowledge Basically the production function is a technological or engineering concept which can be expressed in the form of a table, graph and equation showing the amount of output obtained from various combinations of inputs used in production, given the state of technology. Algebraically, it may be expressed in the form of an equation as

Q = F (L, M, N, C, T̅)

where Q stands for the output of a good per unit of time, L for labour, M for management (of organisation), N for land (or natural resources), С for capital and T̅ for given technology and F refers to the functional relationship function with many inputs cannot be depicted on a diagram.

Economists, therefore, use a two-input production function. If we take two₄ inputs, labour and capital, the production function assumes the form.

Q = F (L, C)

Such a production function is shown in Figure 1.

The production function as determined by technical conditions of production is of two types: it may be rigid or flexible. The former relates to the short-run and the latter to the long-run. In the short-run, the technical conditions of production are rigid so that the various inputs used to produce a given output are in fixed proportions.

However, in the short-run, it is possible to increase the quantities of one input while keeping the quantities of other inputs constant in order to have more output. This aspect of the production function is known as the Law of Variable Proportions. In the long-run, it is possible for a firm to change all inputs up or down in accordance with its scale. This is known as returns to scale.

The returns to scale are constant when output increases in the same proportion as the increase in the quantities of inputs. The returns to scale are increasing when the increase in output is more than proportional to the increase in inputs. They are decreasing if the increase in output is less than proportional to the increase in inputs.

Let us illustrate the case of constant returns to scale with the help of our production function:

Q = (L, M, N, C, T)

Given T̅, if the quantities of all inputs L, M, N, С are increased n-fold, the output Q also increases n-fold. Then the production function becomes

nQ =f (nL, nM, nN, nC)

This is known as the linear and homogeneous production function, or a homogeneous function of the first degree. If the homogeneous function is of the first degree, the production function is

n^k. Q = f (nL, nM, nN, nC)

If k is equal to 1, it is a case of constant returns to scale, if it is greater than 1, it is a case of increasing returns to scale, and if it is less than 1, it is a case of decreasing returns to scale.

Thus a production function is of two types:

(i) Linear homogeneous of the first degree in which the output would change in exactly the same proportion as the change in inputs. Doubling the inputs would exactly double the output, and vice versa. Such a production function expresses constant returns to scale,

(ii) Non- homogeneous production function of a degree greater or less than one. The former relates to increasing returns to scale and the latter to decreasing returns to scale. One of the important production functions based on empirical hypothesis is the Cobb-Douglas production function.

Originally, it was applied to the whole manufacturing industry in America though it can be applied to the whole economy or to any of its sectors. The Cobb-Douglas production functions is

Q = A С^a L^1-a where Q stands for output, L for labour, С for capital employed, A and a are positive constants. In this function, the exponents of L and С added together are equal to 1.

Conclusion:

The production function exhibits technological relationship between physical inputs and outputs and is thus said to belong to the domain of engineering. Prof. Stigler does not agree with this commonly held view. The function of an entrepreneur is to sort out the right type of combination of inputs for the quantity of output he desires.

For this he has to know the prices of his inputs and the technique to be used for producing a specified output within a specified period of time. All these technical possibilities are derived from applied sciences, but cannot be worked out by engineers alone. The production function is, in fact, “the economist’s summary of technological knowledge”, as pointed out by Prof. Stigler.

The Law of Variable Proportions:

If one input is variable and all other inputs are fixed the firm’s production function exhibits the law of variable proportions. If the number of units of a variable factor is increased, keeping other factors constant, how output changes is the concern of this law. Suppose land, plant and equipment are the fixed factors, and labour the variable factor.

When the number of labourers is increased successively to have larger output, the proportion between fixed and variable factors is altered and the law of variable proportions sets in.

According to Prof. Left-witch, “The law of variable proportions states that if a variable quantity of one resource is applied to a fixed amount of other input, output per unit of variable input will increase but beyond some point the resulting increases will be less and less, with total output reaching a maximum before it finally begins to decline.”

This principle can also be defined thus: When more and more units of the variable factor are used, holding the quantities of a fixed factor constant, a point is reached beyond which the marginal product, then the average and finally the total product will diminish.

The law of variable proportions (or the law of non-proportional returns) is also known as the law of diminishing returns. But, as we shall see below, the law of diminishing returns is only one phase of the more comprehensive law of variable proportions.

Its Assumptions:

This law is based on the following assumptions:

(1) It is possible to change the proportions in which the various factors (inputs) are combined.

(2) Only one factor is variable while others are held constant.

(3) All units of the variable factor are homogeneous.

(4) There is no change in technology.

(5) It assumes a short-run situation.

(6) The product is measured in physical units, i.e.. in quintals , tonnes, etc.

(7) The price of the product is given and constant.

Explanation of the Law:

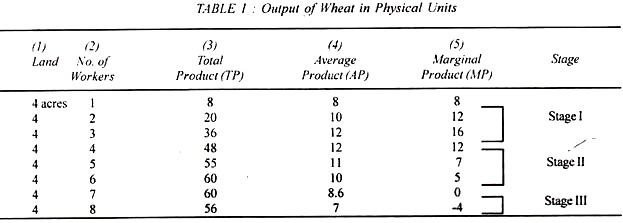
Let us illustrate the law with the help of Table 1, where on the fixed factor (input) land of 4 acres units of the variable factor labour are employed and the resultant output is obtained. The production function is revealed in the first two columns. The average product and marginal product columns are derived from the total product column.

The average product per worker is obtained by dividing column (2) by a corresponding unit in column (1) The marginal product is the addition to total product by employing an extra worker. For instance, 3 workers produce 36 units and 4 produce 48 units. Thus the marginal product is 12 – (48-36) units.

An analysis of the Table shows that the total, average and marginal products increase a maximum and then start declining. The total product reaches its maximum when 7 units of labour are used and then it declines. The average product continues to rise till the 4th unit while the marginal product reaches its maximum at the 3rd unit of labour, then they also fall.

It should be noted that the point of falling output is not the same for total, average and marginal product. The marginal product starts declining first, the average product following it and the total product is the last to fall. This observation points out that the tendency to diminishing returns is ultimately found in the three productivity concepts.

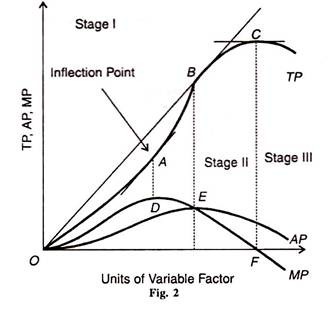
The law of variable proportions is presented diagrammatically in Figure 2. The TP curve first rises at an increasing rate up to point A where its slope is the highest. From point A upwards, the total product increases at a diminishing rate till it reaches its highest point С and then it starts falling.

Point A where the tangent touches the TP curve is called the inflection point up to which the total product increases at an increasing rate and from where it starts increasing at a diminishing rate.

The marginal product curve (MP) and the average product curve (AP) also rise with TP. The MP curve reaches its maximum point D when the slope of the N curve is the maximum at point A. The maximum point on the AP curve is E where it coincides with the MP curve. This point also coincides with point В on the TP curve from where the total product starts a gradual rise.

When the IP curve reaches its maximum point C, the MP curve becomes zero at point F. When the TP starts declining the MP curve becomes negative i.e. is below X-axis. It is only when the total product declines the average product becomes zero i.e. touches the X-axis. The rising, the falling and the negative phases of the total, marginal and average products are, in fact, the different stages of the law of variable proportions which are discussed below.

Stage-I: Increasing Returns:

In stage I, the average product reaches the maximum and equals the marginal product when 4 workers are employed, as shown in Table 1. This stage is portrayed in the figure from the origin to point E where the MP and AP curves meet.

In this stage, the TP curve also increases rapidly. Thus this stage relates to increasing average returns. Here land is too much in relation to the workers employed. It is, therefore, uneconomical to cultivate land in this stage. 

The main reason for increasing returns in the first stage is that in the beginning the fixed factor is large in quantity than the variable factor. When more units of the variable factor are applied to a fixed factor, the fixed factor is used more intensively and production increases rapidly.

It can also be explained in another way. In the beginning the fixed factor cannot be put to the maximum use due to the non-applicability of sufficient units of the variable factor. But when units of the variable factor are applied in sufficient quantities, division of labour and specialization lead to per unit increase in production and the law of increasing returns operate.

Another reason for increasing returns is that the fixed factor is indivisible which means that it must be used in a fixed minimum size. When more units of the variable factor are applied on such a fixed factor, production increases more than proportionately. This cause points towards the law of increasing returns.

Stage-II: Law of Diminishing Returns:

In between stages I and III is the most important stage of production that of diminishing returns. Stage II starts when the average product is at its maximum to the zero point of the marginal product. At the latter point, the total product is the highest.

Table 1 show this stage when the workers are increased from four to seven to cultivate the given land, in Figure 2 between EB and FC. Here land is scarce and is used intensively. More and more workers are employed in order to have larger output.

Thus the total product increases at a diminishing rate and the average and marginal products decline. Throughout this stage, the marginal product is below the average product. This is the only stage in which production is feasible and profitable.

Hence it is not correct to say that the law of variable proportions is another name for the law of diminishing returns. In fact, the law of diminishing returns is only one phase of the law of variable proportions.

Stage-III: Negative Marginal Returns:

Production cannot take place in Stage III either. For, in this stage, total product starts declining and the marginal product becomes negative. The employment of the 8th worker actually causes a decrease in total output from 60 to 56 units and makes the marginal product minus 4.

In the figure, this stage starts from the dotted line FC where the MP curve is below the X-axis. Here the workers are too many in relation to the available land, making it absolutely impossible to cultivate it. To the right of point F, the variable input is used excessively. Therefore, production will not take place in this stage.

The Best Stage:

In stage I, when production takes place to the left of point E in the figure, the fixed factor (land) is too much in relation to the variable factor (workers employed). It is, therefore, uneconomical to use the fixed factor optimally because both the average product (AP) and total production (TP) are increasing.

Therefore, it is in the interest of the producers to produce more. In stage III, when production lakes place to the right of point F in the figure, the variable factor is too much in relation to the fixed factor.

Therefore, no producer will produce in this stage and employ more units of the variable factor beyond the point of zero marginal products (MP) because there is reduction in total product (TP). Thus stages I and III are of economic absurdity or economic nonsense.

So production will always take place in stage II in which the total product is increasing at a diminishing rate and AP and MP are the maximum, then they start decreasing and the total product (TP) is the maximum. Thus the stage of diminishing returns is the optimum and the best stage of production.

The Law of Diminishing Returns:

Benham defines the law of diminishing returns thus: “As the proportion of one factor in a combination of factors is increased, after a point, the average and marginal product of that factor will diminish.”

It’s Application:

Marshall applied the operation of this law to agriculture fisheries, mining, forests and the building industry. He defined the law in these words, “An increase in the capital and labour applied in the cultivation of land causes in general a less than proportionate increase in the amount of produce raised, unless it happens to coincide with an improvement in the arts of agriculture.”

It applies to agriculture both in its intensive and extensive forms. The application of additional units of labour and capital to a piece of land causes diminishing returns. Similarly, increasing the proportion of land in relation to doses of labour and capital causes diminishing return. This is because in agriculture close supervision is not possible. Possibilities of division of labour and the use of machines are limited.

Natural calamities like rain, climate, drought, pests, etc. hinder agricultural operations and bring about diminishing returns. Lastly, agriculture is a seasonal industry. So labour and capital cannot be worked to their full capacity. As a result, costs increase in proportion to the product produced. That is why it is also called the law of increasing costs.

This law also applies to river or tank fisheries where the application of additional doses of labour and capital does not bring a proportionate increase to the amount of fish caught. As more and more fish are caught, the quantity of fish decreases because their quantity is limited in a river or tank. In the case of mines and brick­fields, the continued application of labour and capital will result in diminishing rate of return.

This is because costs will rise in proportion to the yield from the mines as mining operations are carried deep into the mines. So is the case with forest wealth. In order to get more wood, one has to go deep into the forest which requires clearing of shrubs, paying of ways and handling of wood.

These operations require more and more units or labour and capital, thereby increasing the costs in proportion to the output obtained. Further, the law applies to the construction of buildings.

The construction of a multi-storeyed building or sky-scraper requires additional expenses for providing artificial light and ventilation to the lower storeys and power-lifts to reduce the inconvenience of going to the higher floors. It means increase in costs and diminishing returns.

The Law in General Form:

But the law of diminishing returns is not applicable to agriculture and extractive industries alone, rather it is of universal applicability. It is called the law in its general form, which states that if the proportion in which the factors of production are combined is disturbed, the average and marginal product of that factor will diminish.

The distortion in the combination of factors may be either due to the increase in the proportion of one factor in relation to the others or due to the scarcity of one in relation to the other factors.

In either case, diseconomies of production set in, which raise costs and reduce output. For instance, if plant is expanded by installing more machines, it may become unwieldy. Entrepreneurial control and supervision become lax, and diminishing returns set in. Or, there may arise scarcity or trained labour or raw material that leads to diminution in output.

In fact, it is the scarcity of one factor in relation to other factors which is the root cause of the law of diminishing returns. The element of scarcity is found in factors because they cannot be substituted for one another.

Mrs. Joan Robinson explains it thus:

“What the Law of Diminishing Returns really states is that there is a limit to the extent to which one factor of production can be substituted for another, or, in other words, that the elasticity of substitution between factors is not infinite.”

Suppose there is scarcity of jute, since no other fibre can he substituted for it perfectly, costs will rise with production, and diminishing returns will operate.

This is because jute is not in perfectly elastic supply to the industry. If the scarce factor is rigidly fixed and it cannot he substituted by any other factor at all, diminishing returns will at once set in.

If in a factory operated by electric power, there being no other substitute for it, frequent power breakdowns occur, as is commonly the case in India, production will fall and costs will raise in proportion as fixed costs will continue to be incurred even if the factory works for fewer hours than before.

Importance:

In the words of Wick steed, the law of diminishing returns “is as universal as the law of life itself.” The universal applicability of this law has taken economics to the realm of science.

It forms the basis of a number of doctrines in economics. The Malthusian theory of population stems from the fact that food supply does not increase faster than the growth in population because of the operation of the law of diminishing returns in agriculture. In fact, this law was responsible for Malthus’ pessimism.

Ricardo also based his theory of rent on this principle. Rent arises in the Ricardian sense because the operation of the law of diminishing returns on land forces the application of additional doses of labour and capital on a piece of land does not increase output in the same proportion due to the operation of this law.

Similarly, the law of diminishing marginal utility in the theory of demand and that of diminishing marginal physical productivity in the theory of distribution are also based on this doctrine.

In Underdeveloped Countries:

Above all, it is of fundamental importance for understanding the problems of underdeveloped countries. In such economies agriculture is the main occupation of the people. The pressure of population on land increases with the increase in population. As a result, more and more persons are employed on land which is a fixed factor.

This leads to declining marginal productivity of workers. If this process continues and still more labour is added to land, the marginal productivity may become zero or even negative. This explains the operation of the law of diminishing returns in underdeveloped countries in its intensive form.

The Law of Returns to Scale:

The law of returns to scale describes the relationship between outputs and the scale of inputs in the long- run when all the inputs are increased in the same proportion. According to Roger Miller, the law of returns to scale refers “to the relationship between changes in output and proportionate changes in all factors of production.”

To meet a long-run change in demand, the firm increases its scale of production by using more space, more machines and labourers in the factory.

Assumptions:

This law assumes that

(1) All factors (inputs) are variable but enterprise is fixed.

(2) A worker works with given tools and implements.

(3) Technological changes are absent.

(4) There is perfect competition.

(5) The product is measured in quantities.

Explanation:

Given these assumptions, when all inputs are increased in unchanged proportions and the scale of production is expanded, the effect on output shows three stages.

Firstly, returns to scale increase because the increase in total output is more than proportional to the increase in all inputs.

Secondly, returns to scale become constant as the increase in total product is in exact proportion to the increase in inputs.

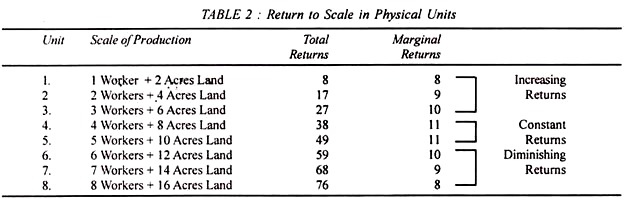
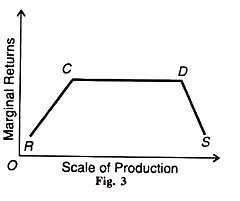
Lastly, returns to scale diminish because the increase in output is less than proportionate to the increase in inputs. This principle of returns to scale is explained with the help of Table 2 and Figure 3.

This table reveals that in the beginning with the scale of production of (1 worker + 2 acres of land), total output is 8. To increase output when the scale of production is doubled (2 workers + 4 acres of land), total returns are more than doubled. They become 17.

Now if the scale is trebled (3 workers + 6 acres of land), returns become more than three-fold, i.e., 27. It shows increasing returns to scale. If the scale of production is increased further, total returns will increase in such a way that the marginal returns become constant.

In the case of the 4th and 5th units of the scale of production, marginal returns are 11, i.e., returns to scale are constant. The increase in the scale of production beyond this will lead to diminishing returns. In the case of the 6th, 7th and 8th units, the total returns increase at a lower rate than before so that the marginal returns start diminishing successively to 10, 9 and 8.

In Figure 3, RS is the returns to scale curve where from R to С returns are increasing, from С to D, they are constant and from D onwards they are diminishing. Why do returns to scale first increase, become constant, and then diminish?

(1) Increasing Returns to Scale:

Returns to scale increase because of the indivisibility of the factors of production. Indivisibility m6ans that machines, management, labour, finance, etc., cannot be available in very small sizes. They are available only in certain minimum sizes. When a business unit expands, the returns to scale increase because the indivisible factors are employed to their maximum capacity.

Increasing returns to scale also result from specialisation and division of labour. When the scale of the firm is expanded there is wide scope of specialization and division of labour. Work can be divided into small tasks and workers can be concentrated to narrower range of processes. For this, specialised equipment can be installed. Thus with specialisation, efficiency increases and increasing returns to scale follow.

Further, as the firm expands, it enjoys internal economies of production. It may be able to install better machines, sell its products more easily, borrow money cheaply, procure the services of more efficient manager and workers, etc. All these economies help in increasing the returns to scale more than proportionately.

Not only this, a firm also enjoys increasing returns to scale due to external economies. When the industry itself expands to meet the increased long-run demand for its product, external economies appear which are shared by all the firms in the industry.

When a large number of firms are concentrated at one place, skilled labour, credit and transport facilities are easily available. Subsidiary industries crop up to help the main industry. Trade journals, research and training centres appear which help in increasing the productive efficiency of the firms. Thus these external economies are also the cause of increasing returns to scale.

(2) Constant Returns to Scale:

But increasing returns to scale do not continue indefinitely. As the firm is enlarged further, internal and external economies are counterbalanced by internal and external diseconomies. Returns increase in the same proportion so that there are constant returns to scale over a large of output.

Here the curve of returns to scale is horizontal (see CD in Figure 3). It means that the increments of each input are constant at all levels of output. Further, when factors of production are perfectly divisible, substitutable, and homogeneous with perfectly elastic supplies at given prices, returns to scale are constant.

(3) Diminishing Returns to Scale:

Constant returns to scale are only a passing phase, for ultimately returns to scale start diminishing. Indivisible factors may become inefficient and less productive. Business may become unwieldy and produce problems of supervision and coordination.

Large management creates difficulties of control and rigidities. To these internal diseconomies are added external diseconomies of scale. These arise from higher factor prices or from diminishing productivities of the factors. As the industry continues to expand, the demand for skilled labour, land, capital, etc. rises.

There being perfect competition, intensive bidding raises wages, rent and interest. Prices of raw materials also go up. Transport and marketing difficulties emerge. All these factors tend to raise costs and the expansion of the firms leads to diminishing returns to scale so that doubling the scale would not lead to doubling the output.

In reality, it is possible to find cases where all factors have tended to increase. Whereas all inputs have increased, enterprise has remained unchanged. In such a situation, changes in output cannot be attributed to a change in scale alone. It is also due to a shift in factor proportions. Thus, the law of variable proportions is applicable in the real world.