The Cobb-Douglas Production Function

The below mentioned article provides a close view on the Cobb-Douglas Production Function.

The Cobb-Douglas production function is based on the empirical study of the American manufacturing industry made by Paul H. Douglas and C.W. Cobb. It is a linear homogeneous production function of degree one which takes into account two inputs, labour and capital, for the entire output of the .manufacturing industry.

The Cobb-Douglas production function is expressed as:

Q = AL^a C^β

where Q is output and L and С are inputs of labour and capital respectively. A, a and β are positive parameters where = a > O, β > O.

The equation tells that output depends directly on L and C, and that part of output which cannot be explained by L and С is explained by A which is the ‘residual’, often called technical change.

The production function solved by Cobb-Douglas had 1/4 contribution of capital to the increase in manufacturing industry and 3/4 of labour so that the C-D production function is

Q = AL^3/4 C1^/4

which shows constant returns to scale because the total of the values of L and С is equal to one: (3/4 + 1/4), i.e.,(a + β = 1) . The coefficient of labourer in the C-D function measures the percentage increase in (Q that would result from a 1 per cent increase in L, while holding С as constant.

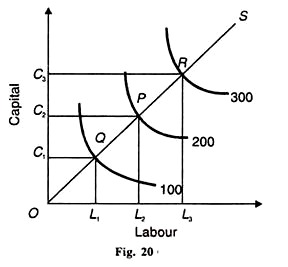
Similarly, В is the percentage increase in Q that would result from a 1 per cent increase in C, while holding L as constant. The C-D production function showing constant returns to scale is depicted in Figure 20. Labour input is taken on the horizontal axis and capital on the vertical axis.

To produce 100 units of output, ОС, units of capital and OL units of labour are used. If the output were to be doubled to 200, the inputs of labour and capital would have to be doubled. ОС is exactly double of ОС₁ and of OL₂ is double of OL_2.

Similarly, if the output is to be raised three-fold to 300, the units of labour and capital will have to be increased three-fold. OC₃ and OL₃ are three times larger than ОС₁, and OL₁, respectively. Another method is to take the scale line or expansion path connecting the equilibrium points Q, P and R. OS is the scale line or expansion path joining these points.

It shows that the isoquants 100, 200 and 300 are equidistant. Thus, on the OS scale line OQ = QP = PR which shows that when capital and labour are increased in equal proportions, the output also increases in the same proportion.

Criticisms of C-D Production Function:

The C-D production function has been criticised by Arrow, Chenery, Minhas and Solow as discussed below:

1. The C-D production function considers only two inputs, labour and capital, and neglects some important inputs, like raw materials, which are used in production. It is, therefore, not possible to generalize this function to more than two inputs.

2. In the C-D production function, the problem of measurement of capital arises because it takes only the quantity of capital available for production. But the full use of the available capital can be made only in periods of full employment. This is unrealistic because no economy is always fully employed.

3. The C-D production function is criticised because it shows constant returns to scale. But constant returns to scale are not an actuality, for either increasing or decreasing returns to scale are applicable to production.

It is not possible to change all inputs to bring a proportionate change in the outputs of all the industries. Some inputs are scarce and cannot be increased in the same proportion as abundant inputs. On the other hand, inputs like machines, entrepreneurship, etc. are indivisible. As output increases due to the use of indivisible factors to their maximum capacity, per unit cost falls.

Thus when the supply of inputs is scarce and indivisibilities are present, constant returns to scale are not possible. Whenever the units of different inputs are increased in the production process, economies of scale and specialization lead to increasing returns to scale.

In practice, however, no entrepreneur will like to increase the various units of inputs in order to have a proportionate increase in output. His endeavour is to have more than proportionate increase in output, though diminishing returns to scale are also not ruled out.

4. The C-D production function is based on the assumption of substitutability of factors and neglects the complementarity of factors.

5. This function is based on the assumption of perfect competition in the factor market which is unrealistic. If, however, this assumption is dropped, the coefficients α and β do not represent factor shares.

6. One of the weaknesses of C-D function is the aggregation problem. This problem arises when this function is applied to every firm in an industry and to the entire industry. In this situation, there will be many production functions of low or high aggregation. Thus the C-D function does not measure what it aims at measuring.

Conclusion:

Thus the practicability of the C-D production function in the manufacturing industry is a doubtful proposition. This is not applicable to agriculture where for intensive cultivation, increasing the quantities of inputs will not raise output proportionately. Even then, it cannot be denied that constant returns to scale are a stage in the life of a firm, industry or economy. It is another thing that this stage may come after some time and for a short while.

It’s Importance:

Despite these criticisms, the C-D function is of much importance.

1. It has been used widely in empirical studies of manufacturing industries and in inter-industry comparisons.

2. It is used to determine the relative shares of labour and capital in total output.

3. It is used to prove Euler’s Theorem.

4. Its parameters a and b represent elasticity coefficients that are used for inter-sectoral comparisons.

5. This production function is linear homogeneous of degree one which shows constant returns to scale, If α + β = 1, there are increasing returns to scale and if α + β < 1, there are diminishing returns to scale.

6. Economists have extended this production function to more than two variables.