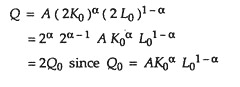Homogeneous Production Function| Economics

A function is said to be homogeneous of degree n if the multipli­cation of all the independent variables by the same constant, say λ, results in the multiplication of the dependent variable by λⁿ. Thus, the function

Y = X² + Z²

is homogeneous of degree 2 since

(λX)² + (λZ)² = λ² (X² + Y²) = λ²Y

A function which is homogeneous of degree 1 is said to be linearly homogeneous, or to display linear homogeneity. A production function which is homogeneous of degree 1 displays constant returns to scale since a doubling all inputs will lead to an exact doubling of output. So, this type of production function exhibits constant returns to scale over the entire range of output. In general, if the production function Q = f (K, L) is linearly homogeneous, then

F (λK, λL) = λf (K ,L) = λQ

for any combination of labour and capital and for all values of λ. If λ equals 3, then a tripling of the inputs will lead to a tripling of output.

There are various examples of linearly homogeneous functions.

Two such examples are the following:

Q = aK + bL

and Q = A K^α L^1-α 0 < α < 1

The second example is known as the Cobb-Douglas production function. To see that it is, indeed, homogeneous of degree one, suppose that the firm initially produces Q₀ with inputs K₀ and L₀ and then doubles its employ­ment of capital and labour.

The resulting output would equal:

This shows that the Cobb-Douglas production function is linearly homo­geneous.

Properties:

There are various interesting properties of linearly homoge­neous production functions. First, we can express the function, Q = f (K,L) in either of two alternative forms.

(1) Q = Kg (L/K) or,

(2) Q = Lh (K/L)

This property is often used to show that marginal products of labour and capital are functions of only the capital-labour ratio.

In particular, the marginal products are as follows:

MP_k = g (L/K) – (L/K) g’ (L/K)

and MP_L = g’ (L/K)

where g’ (L, K) denotes the derivative of g (L/K). The significance of this is that the marginal products of the inputs do not change with proportionate increases in both inputs. Since the marginal rate of technical substitution equals the ratio of the marginal products, this means that the MRTS does not change along a ray through the origin, which has a constant capital- labour ratio. Since the MRTS is the slope of the isoquant, a linearly homo­geneous production function generates isoquants that are parallel along a ray through the origin.

Expansion Path:

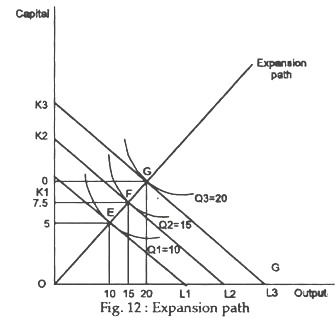
If a firm employs a linearly homogeneous production function, its expan­sion path will be a straight line. To verify this point, let us start from an initial point of cost minimisation in Fig.12, with an output of 10 units and an employment (usage) of 10 units of labour and 5 units of capital. Now, suppose, the firm wants to expand its output to 15 units. Since input prices do not change, the slope of the new iso­quant must be equal to the slope of the original one.

But, the slope of the isoquant is the MRTS, which is constant along a ray from the origin for linearly ho­mogeneous production function. Consequently, the cost minimising capital-labour ratio will remain constant. Since output has increased by 50%, the inputs will also increase by 50% from 10 units of labour to 15 and from 5 units of capital to 7.5. Thus, the expansion path is a straight line.

Production functions may take many specific forms. Typically economists and researchers work with homogeneous production function. A function is said to be homogeneous of degree n if the multiplication of all of the independent variables by the same constant, say λ, results in the multiplication of the independent variable by λⁿ. Thus, the function:

Q = K² + L²

is homogeneous of degree 2 since

(λK)² + (λ L)² = λ² (K² + L²) = λ²Q

A function which is homogeneous of degree 1 is said to be linearly homogeneous, or to display linear homogeneity. A production function which is homogeneous of degree 1 displays constant returns to scale since a doubling all inputs will lead to a doubling of output.

A production function is homogeneous of degree n if when inputs are multiplied by some constant, say, α, the resulting output is a multiple of a² times the original output.

That is, for a production function:

Q = f (K, L)

then if and only if

Q = f (αK, αL) = αⁿf (K, L)

is the function homogeneous. The exponent, n, denotes the degree of homo­geneity. If n=1 the production function is said to be homogeneous of degree one or linearly homogeneous (this does not mean that the equation is linear). A linearly homogeneous production function is of interest because it exhib­its CRS.

This is easily seen since the expression αⁿ. f(K, L) when n=1 reduces to α. (K, L) so that multiplying inputs by a constant simply increases output by the same proportion. Examples of linearly homogeneous production functions are the Cobb-Douglas production function and the constant elas­ticity of substitution (CES) production function. If n > 1, the production function exhibits IRS. If n< 1 DRS prevails.

Cobb-Douglas Production Function:

Economists have at different times examined many actual production func­tions and a famous production function is the Cobb-Douglas production function. Such a function is an equation showing the relationship between the input of two factors (K and L) into a production process, and the level of output (Q), in which the elasticity of substitution between two factors is equal to one.

As applied to the manufacturing production, this production function, roughly speaking, states that labour contributes about three-quar­ters of the increases in manufacturing production and capital the remaining one-quarter.

Suppose, the production function is of the following type:

Q = AK^α L^β

where Q is output, A is constant, K is capital input, L is labour input and a and (3 are the exponents of the production function. This is known as the Cobb-Douglas production function. It has an important property.

The sum of the two exponents indicates the returns to scale:

(i) If α + β > 1, the production function exhibits increasing returns to scale,

(ii) If α + β = 1, there are constant returns to scale,

(iii) Finally, if α + β < 1, there are decreasing returns to scale.

Suppose, the production is of the following type:

Q = AK^0.+75 L^0.25

It exhibits constant return to scale because α = 0.75 and β = 0.25 and α + β = 1.