In this article we will discuss about:- 1. Least Cost Combination of Inputs 2. Maximum Output Combination of Inputs.
Least Cost Combination of Inputs:
The firm may produce a particular quantity of its product at each of the alternative input combinations that lies on the IQ for that quantity. Since the firm’s goal is to maximise profit, the optimum input combination for producing a particular quantity of its product would be one that would produce the output at the minimum possible cost.
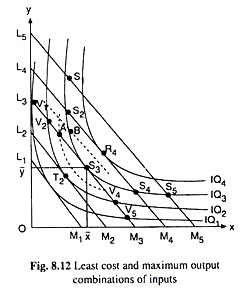
The optimum input combination in this case is known as the least cost combination of inputs. In order to explain the firm’s selection of the least cost combination of inputs, let us suppose that some of the firm’s isoquants (IQs) and iso-cost lines (ICLs) are given in Fig. 8.12.
Let us now suppose that the firm intends to produce a particular quantity q = q3 of its product, and the isoquant for this particular quantity is IQ3. In other words, if the firm uses any of the input combinations lying on IQ3, it would be able to produce the output quantity q = q3.
ADVERTISEMENTS:
But, since the different points on IQ3, viz., S1, S2, S3, S4, S5, etc. lie on different ICLs, they produce the same output, viz., q = but at different levels of cost, For we know that a higher (or a lower) ICL represents a higher (or a lower) level of cost.
Therefore, in order to produce the output of q3 at the least possible cost, the firm would have to select that point on IQ3 that would lie on the lowest possible ICL. In Fig. 8.12, we see that the point S3 on IQ3 lies on the lowest possible ICL, viz., L3M3. Any other point on IQ3 lies on a higher ICL or a higher level of cost than L3M3.
Therefore, at an output of q3, the least cost combination of inputs is S3(x̅, y̅). In other words, if the firm is to produce an output of q3, it would buy and use the quantity x of input X and the quantity y of input Y. Here it is very important for us to observe that the least cost combination of inputs is the point of tangency (here S3) between the particular isoquant (here IQ3) and an iso-cost line (here L3M3).
Similarly, for producing a particular quantity of output, if the firm is to remain on IQ2, then the least cost combination of inputs would be given by the point T2, because this point is the point of tangency between IQ2 and an ICL (i.e., L2M2).
Maximum Output Combination of Inputs:
ADVERTISEMENTS:
In iso-cost lines (ICLs), we have seen that if the prices (rX and rY) of the inputs (X and Y) are given and constant, then by spending a particular amount of money the firm can buy any one of a large number of input combinations that lie on the corresponding ICL.
Since the firm’s goal is to maximise the level of profit, the optimum input combination in this case would be one that would produce the maximum possible output. Therefore, this input combination is called the maximum- output combination of inputs.
We shall now see with the help of Fig. 8.12, how the maximum output-input combination can be obtained by the firm. Let us suppose that the firm has decided to spend a particular amount of money, TVC3, (TVC stands for total variable cost) for the two variable inputs (X and Y), and the ICL for this expenditure is L3M3.
That is, if the firm is to spend the amount of money TVC3, then it would have to buy some combination that lie on the iso-cost line, L3M3.
Now the points like V1, V2 S3, V4, V5 lying on L3M3 are situated on different isoquants. That is, at different points on the line L3M3, the cost of the firm is the same (= TVC3), but the quantities produced are different.
Since a higher IQ represents a higher level of output, of all the points on L3M3, the profit-maximising firm would select that one as optimum which lies on the highest possible IQ, i.e., which produces the highest possible level of output. This point is S3 (x̅, y̅) on, IQ3—this point is the maximum-output Combination of inputs subject to the cost constraint of TVC = TVC3.
We have to note here that the maximum-output combination of inputs subject to the cost constraint (here S3) is the point of tangency between the ICL corresponding to the given cost level (here TVC3) and an IQ (here IQ3).
Similarly, if the given ICL of the firm is L4M4, then the maximum-output combination of inputs would be the point R4, because this point is the point of tangency between the line L4M4 and an IQ which is here IQ4.