H-O Theory of International Trade | Economics

In this essay we discuss the H-O theory of international trade which is essentially the mod­ern theory of comparative advantage. And, like the Ricardian theory, the H-O theory explains the basis of trade between two countries by focusing on differences in supply conditions.

Eli Hechscher and Bertil Ohlin explained the basis of trade between two countries on the basis of differences in relative factor endowments. They developed a theory that highlights the variations among countries of supplies of certain main categories of productive factors (labour, capital, and land, none of which is specific to any one sector).

Assumptions:

The H-O analysis is based on a number of assumptions:

1.2 x 2 x 2 Case:

There are 2 countries, 2 homogeneous goods, and 2 homogeneous factors of production. The initial levels of such factors remain fixed and are assumed to be relatively different for each country.

2. Identical Technology:

Technology is the same in both countries. This means that 2 coun­tries have the same production functions.

3. Constant Returns:

Production in each country takes place under conditions of CRS for both the commodities.

4. Different Factor Intensities:

The two commodities have different factor intensities. But the respective commodity intensities are the same for all factor price ratios.

5. Identical and Homothetic Taste and Preference:

Tastes and preferences are the same in both countries. In addition, they are homothetic in nature which means that the two commodi­ties are consumed in the same relative ratios at all income levels.

6. Perfect Competition:

Perfect competition exists in the product markets of both countries.

7. Perfect Factor Mobility:

Factors are perfectly mobile within each country but not be­tween countries.

8. Absence of Transport Costs:

There are no transport costs.

9. No Trade Barriers:

There is no government restriction on the movement of goods be­tween countries or interference with the market determinants of prices and output.

10. Strong Factor Abundance Assumption:

Finally, we assume that the countries that are labour-abundant (i.e., that have labour force that are large relative to their capital stocks), will have low wages relative to rental payments, and vice versa for capital-abundant countries. This is known as Paul Samuelson’s strong factor abundance assumption. The implication of this assumption will be clear when we compare the physical definition of factor abundance with the price definition.

Two of the above assumptions are critical to the H-O explanation of the basis of trade, viz., assumption 1 (that factor endowments or availabilities differ between two countries) and as­sumption 4 (commodities are always intensive in a given factor regardless of relative factor prices). These assumptions have to be discussed in further detail.

Meaning of Factor Abundance:

The term ‘different factor endowments’ refers to different relative factor endowments, not dif­ferent absolute amounts. The basic implication key assumption of 4 is that factor proportions are difference between the two countries. Relative factor abundance may be defined in two ways: the physical definition and the price definition.

Physical Definition and Price Definition:

The physical definition explains factor abundance in terms of the physical units of two factors, for, e.g., labour and capital, possessed by the two countries. Country 1 would be treated as capital-abundant if its ratio of capital to labour (K/L) exceeded the same ratio in country 2 [(K/L)₁ > (K/L) ₂]. Similarly, a country is relatively labour abundant if the total work force relative to the capi­tal stock is greater there than in the other country [(L/K)₂ > (LIK)₁].

It is the relative amount of factors which counts, not the size of a country. A country with fewer absolute units of physical capital than a larger country could still be the capital-abundant country as long as the amount of capital relative to labour was greater than the same ratio in the larger country. Finally, since the position of a country is always relative, not absolute, in the two-country case, if country 1 is the capital-abundant country, then country 2 must be the labour-abundant country.

Relative differences matter here. Thus, a country cannot be labour-abundant simply by having a large population. We have also to take into account the country’s capital stock. More simply, ratios are important, not levels.

The price definition is based on the relative prices of capital and labour to determine the relative factor abundance of the two countries. According to the definition, country 1 is the capital-abundant if (r/w)₁ < (r/W)₂, that is, the ratio of the price of capital (rental rate) to the price of labour (wage rate) in country 1 is less than that the same in country 2.

This definition views relative abundance in terms of the relative scarcity price of the two factors. The more abundant a factor is relative to another factor, the lower is its relative price. These two defini­tions are different but interrelated. It is because the greater (or smaller) the supply of a factor, the lower (or higher) its price tends to be.

However, factor prices reflect not only the physical availability of the factors in question but also the structure of final demand and the nature of technology used. Since the H-O model assumes that technology and tastes and preferences are the same in both countries, these two definitions yield the same result. This means that the relatively large K/L ratio will also have the relatively smaller r/w ratio.

Only if mere technology or demand conditions differ between the two countries by the price definition is likely to clearly differ from the physical definition. For example, physical abundant capital may be relatively high-priced. This point will be taken up later in this essay.

Commodity Factor Intensity:

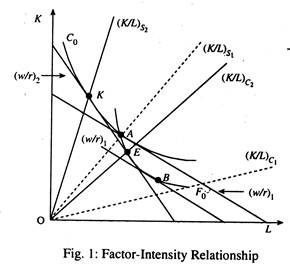
A commodity such as motor car is said to be capital-intensive whenever the ratio of K to L is larger compared with a similar ratio of factor usage of another commodity, such as food. The H-O holds that difference in factor intensities leads to all positive factor price ratios in both countries (and not just at common factor prices). This means that at all possible factor prices, the isoquants reflecting the technology used in car production are more tilted toward the capi­tal axis, compared with the isoquants reflecting food production.

This means that the capital- labour ratio for car will always be larger than that for food. If may be noted that in describing the technology of producing goods we refer to food as the labour -intensive product, while in refer­ring to countries we describe country 2 as the labour-abundant country. In the context of the H-O model we refer to the factor intensity of production and the factor abundance of coun­tries. See Fig. 1.

A key assumption of the H-O analysis is that commodities are intensive in a given fac­tor irrespective of relative factor price. This point is illustrated in case of car (isoquant C₀) and food (isoquant F₀). Given the nature of the isoquant map for each commodity, car will always have a higher K/L than wheat at all fac­tor price ratios and, thus, it is the capital-in­tensive product. If car is relatively capital-intensive, then food has to be labour-intensive. This means that it will always have a relatively smaller K/L compared to car.

This point becomes clear when we compare the K/L of the two goods when labour is relatively cheap [(w/r)] with ratios when labour is relatively expensive [(w/r)₁]. The capital-labour ratio used in production at any point on any isoquant is given by the slope of a ray from the origin through the production point. Thus at (w/r), production of car (at A) is more K-intensive than production of food (at B); at (w/r)₂, production of car (at D) is again more K-intensive than production of food (at E).

The H-O Theorem:

From the set of assumptions about production it follows that the PPC of the two countries will differ solely because their factor endowments differ. With identical technology in both countries—CRS, and a given factor-intensity relationship between the two goods, the capital-abundant country will be able to produce relatively more of the capital-intensive good, and the labour-abundant country will be able to pro­duce relatively more of the labour-intensive good.

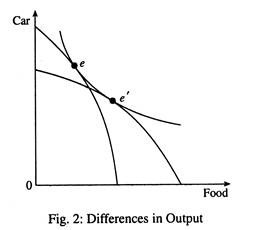
In Fig. 2 the PPC of country 1, the capital-abundant country, is skewed toward the production of capital- intensive good, car. The PPC of country 2, the labour- abundant country, is skewed toward the labour-intensive good—food. Country 1 produces and consumes at point e and country 2 at e.

Their production and consumption points are the same under autarky. Although demand conditions are the same, their consumption levels differ due to differences in production levels, caused by differing factor endowments.

H-O Model and the Factor Price Equalisation (FPE) Theorem:

Perhaps the most controversial theorem of the H-O model is concerned with the effect of trade on factor prices.

This theorem is known as the FPE, which is stated below:

Given all the assumptions of the H-O model free international trade will lead to the interna­tional equalisation of individual factor prices. Under the strict assumptions of the H-O model, the tendencies for factor prices to move up or down will continue until the equalisation of such price is achieved.

It is important to know how strict the H-O conditions are for FPE to occur. To be more specific, all of the assumptions of the H-O model must hold perfectly. Two of the most important of these assumptions are ‘no barriers to trade’ and ‘access to identical technology’.

If workers everywhere have the same productivity, then free trade guarantees that they earn the same wage. However, if there are tariff and non-tariff barriers to trade, then some workers may earn more than their equally productive foreign counterparts. Since neither assumption is perfectly satisfied in the real world, we should not expect complete factor price equalisation.

There is some support, however, for the main predictions of the theorem. Lowering trade barriers between countries has affected income levels in different countries. Trade liberalisa­tion leads to a marked reduction in the dispersion of incomes across countries under conditions of identical technology.

The FPET predicts that some factor payments will rise and others will fall with the intro­duction of trade. In this context, we refer to a related but important issue – the need for incom­plete specialisation to ensure complete FPE.

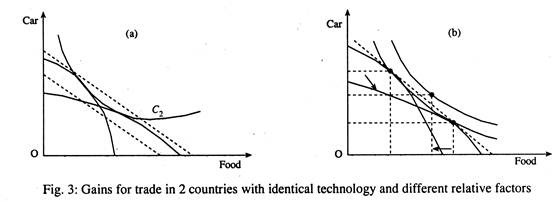
With identical demand conditions, indicated by the common CIC, I₁,₂ the relative price of food (P_F/P_c)₂ in country 2 is less (a flatter relative price line) than that in country 1 (P_F/ P_c)₁. Thus there is a basis of trade between the two countries from the supply side (as is the case in the Ricardian model). Both will gain from trade if the common international price ratio (P_F/P_C) lies between the two domestic (autarkic) price ratios as shown in part (b) of Fig. 3.

Both countries will now be eager to consume at point C, which lies beyond their respective PPC_S. In addition, production will shift to point, P₁ in country 1 and to P₂ in country 2. Country 2 will, therefore, export F₁, F₀ of food and import S₂S₁ of car. Country 1 will export C₁C₀ of car and import F₂F₁ of food.

In equilibrium, export of country 2 (F₁F₀) is the same as import of country 1 (F₂F₁), and export of C₁C₀ of country 1 is the same as country 2 is import of C₂C₁. Thus both countries find themselves better off by being able to move on a higher CIC, C₁ indicating the mutual gain from trade. Each country expands production and export of the good that makes the more intensive use of its relatively abundant factor of production.

So long we were concerned with the physical definition of factor abundance. The price definition of factor abundance also yields the same result. In the capital-abundant country 1, (r/w)₁ < (r/w)₂ for (w/r)₁ > (w/r)₂], With identical technology and CRS, country 1 will be able to produce cars more cheaply than country 2, and country 2 will produce food more cheaply than country 1.

Relationship—Relative Factor Prices and Relative Product Prices:

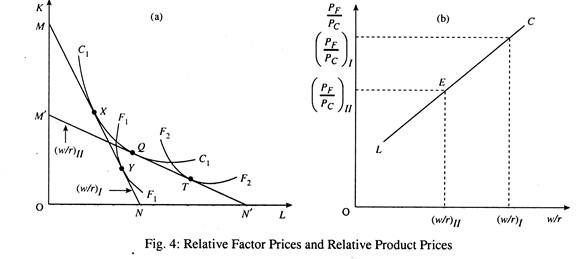
We now can make an important deduction from the H-O analysis. We can establish the rela­tionship between relative factor prices and relative product prices. Relative factor prices (w/r)₁ are shown in part (a) by the isocost line MN. Country 1 will produce C₁ units of car at point X and F₁ units of food at point Y. Since country 2 is a relatively labour-abundant country, its relative factor price ratio (w/r)₂ < (w/r)₁.

So its isocost line M’N’ is flatter than that of country 1. It will, therefore, produce at point Q and point T, at two different relative factor prices. Since F₂ represents a larger quantity of food for the same opportunity cost of car, C₁ the relative price of food must be less in country 2 than in country 1.

In part (b) of Fig. 4 we show the direct link between relative factor prices and relative product prices. An increase in w relative to r will lead to an increase in the price of the labour-intensive good, food, relative to the price of the capital-intensive good, cloth.

If we show relative factor prices on the horizontal axis and relative product prices on the vertical axis, we find a direct relation between the two as is shown by the upward-sloping curve LC. (If car had been the relatively labour-intensive good rather than food, the relationship would be reflected in a downward sloping curve).

Now it is quite clear that different relative factor prices will generate different relative prod­uct prices in autarky. There will, thus, exist a basis for trade. Each country will export the product which it can produce more cheaply: car in country 1 and food in country 2.

The H-O Theorem:

With this H-O analysis, we may now state the H-O theorem as follows:

A country will export the commodity which uses its relative abundant factor more inten­sively and it will import the commodity which uses its relatively scarce factor of production more intensively. Thus, exports are intensive in a country’s abundant factor and imports are intensive in its scarce factor.

The H-O would hold that the direction of international trade flows between two countries is determined by two things:

(1) The endowment of productive factors in the two countries; and

(2) The factor content of the goods involved.

The H-O theorem can be stated more precisely as follows:

A country will have a comparative advantage in, and, therefore, will export that good whose production is relatively intensive in the factor with which the country is relatively well-endowed:

Alternatively stated, the country that is relatively capital-abundant compared with the other country will have a comparative advantage in the good that requires more capital per worker to produce. In this case we would expect that country 1(2) to have a comparative advantage in car (food) production, since we have assumed that country 1(2) is relatively capital (labour) abun­dant and car (food) production is relatively capital (labour) intensive.

The Pattern of Trade Flows:

So far we have shown how comparative advantage is determined in the H-O model. How do we know that trade will flow in the direction of comparative advantage? The answer to the ques­tion is straightforward. In a competitive environment, trade flows are determined by profit- maximising behaviour of economic agents.

A good will tend to be exported to those places where it is relatively expensive. Consequently, we would expect country 1 to export car. Like­wise, exporters in 2 should want to export food to country 1, where it is (at first) relatively more expensive.

Equilibrium in the H-O Model:

We have already considered the effect of the introduction of international trade on the produc­tion and consequent decisions of each of the two countries. Once trade is allowed between two countries, differences in relative prices will not persist. Consequently, price of car will begin to rise in country 1 (where it was initially low) and fall in country 2 (where it was initially high).

As in the Ricardian model only one price – the international price—will prevail once trade begins. This common price is determined by international forces of demand and supply, known as reciprocal demand. These forces establish a price that can prevail simultaneously in devel­oping countries so that desired trade flows are balanced.

After all, if desired trade flows are not balanced, then, by definition, one country wants to trade more than the other, and this will cause prices to move up or down. So at any point in time, only one price will prevail in the international market.

Diagrammatically, the condition for international equilibrium is that the trade triangles of the two countries coincide. This means that the sides of the two triangles are equal in length. This is indeed the case in H-O model as in the Ricardian model, because in a 2-country 2- commodity framework, one country’s export is the other country’s import, and vice versa.

Incomplete Specialisation:

Another characteristic of this trading equilibrium in the H-O model is that neither country completely specialises in the production of the commodity in which it has a comparative ad­vantage. Incomplete specialisation in production is the obvious result of the presence of in­creasing opportunity costs.

This means that as the relative price of a country’s exportable good rise after trade, there is an incentive to produce more of that good. Production will continue to expand so long as the relative cost of expanding production is less than, or just equal to, the relative price. However, with an increase in production, costs also rise.

So, ultimately, a point will be reached beyond which relative costs exceed the relative price. This point acts an obsta­cle to further expansion of production, unless the price were to rise faster than costs.

Comparison with the Classical Model:

In the Ricardian model the PPC of each country is a straight line. This is why complete specialisation in production of only one good is the only logical possibility. But, in the H-O, com­plete specialisation is not likely, but it cannot be ruled out. We know that the production point depends upon the relative price of exportable. It is quite possible that the price could rise so much that all of the economy’s resources could be attracted to the export industry.

Complete specialisation is also likely to occur in production if the two goods were relatively similar in their use of factor inputs, i.e., the factor intensities were the same in the two indus­tries The more similar the techniques used in producing the two goods, the less additional unit of one good is to be sacrificed as factors are increasingly attracted to the other industry.

This means that as goods become more similar in production, the less bowed out are the, and the PPCs tend to become straight lines as are found in the constant-cost classical model-where complete specialisation is the only logical possibility.

Role of Reciprocal Demand:

A more important difference between the Ricardian model and the H-O model is related to the manner in which the process of reciprocal demand leads to an equilibrium international price .We know that once trade begins in the classical model, the production point is fixed at the point complete specialisation.

This means that equilibrium levels of exports and imports are achieved through changes in demand in the two countries. In the H-O model, reciprocal demand leads to an equilibrium price by inducing changes in both demand and supply.

Comparison of the H-O Model with the Ricardian Model:

The following points emerge from a comparison of the H-O model with the Ricardian model.

1. Assumptions about Demand:

The two models differ on the importance of assumptions made about demand. The classical model place no restrictions on assumptions about common tastes in the two countries except consumers are sufficiently cosmopolitan. This means that they consume some of both the roods before and after trade.

Since the autarkic prices in that model are determined solely by supply conditions, so little attention is paid to demand. By contrast, the H-O model assumes that tastes are identical. By ruling out differences in tastes, we prevent tastes from overturning the predictions of the H-O model.

2. Production Conditions:

In the Ricardian model, the only factor of production is labour. In the Ricardian model comparative advantage is determined by production conditions alone. In addition, if a country has a comparative advantage in the production of a good, it will export that good.

In the H-O two-factor model these two conditions are no longer needed. If we define the price definition of factor abundance, the second condition is fulfilled. This means at, a country is abundant in capital, it will also export the capital-intensive good But the first condition is not needed, because we cannot infer from production conditions alone anything about factor prices.

Then if we analyse the physical definition of factor abundance we find that this definition takes into account only production conditions. So the first condition of the Recardian model is fulfilled. But the second is not, because it is not possible to infer anything about comparative advantage. We cannot; for instance, use this definition to predict that the capital-abundant country will export the capital-intensive good.

If we adopt the physical definition of factor abundance we find that a capital-abundant country will produce more of the capital-intensive good than the labour-abundant country. In our example, capital- abundant country 1 will always produce C/F in a higher ratio than country Z It urn this sense that country 1 has a comparative advantage in the production of the capital intensive good and country 2 in the production of the labour intensive good.

The Stolper-Samuelson Theorem:

The Stolper-Samuelson theorem (SST) refers to the effect of the opening up of trade on the pattern of income distribution. The theorem suggests that free trade splits a country into specific gainers and losers.

The theorem states that, given certain conditions and assumptions a shift from no trade to free trade that changes product prices in a country has two clear effects:

1. It raises the real return to the factor used intensively in the rising-price industry

2. It lowers the return to the factor used intensively in the falling-price industry

For example, the opening of trade increases the relative price of car (its export product) in the USA and reduces the price of food (its import item). The SST then predicts a rise in the real income of the owners of capital (the factor used intensively in producing car) and a the real income of the suppliers of labour (the factor used intensively in producing food)In the rest of the world, the real income of labour increases and that of capitalists falls.

The SST can be stated thus:

Any protective measure that raises the domestic price of an imported article must unambiguously benefit the scarce factor used intensively in producing the import-competing good.

This relationship was used initially to describe the impact of tariff protection if imports are labour-intensive. Thus, an increase in the price of a labour-intensive good such as food (with price of cars remaining unchanged) must unambiguously raise the real wages. But the same analysis can be modified to show the effect of import tariff if imports are capital- intensive.

According to the classical (Ricardian) theory of comparative cost (advantage) free trade is better than no trade (autarky) because free trade allows a country to go beyond its PPC and consume more than what it is capable of producing. As a result, the standard of living of the trading nation un-proves.

This means that free trade benefits every citizen and protection hurts everyone. In 1941 Stolper and Samuelson challenged this view and showed that in general those who supply the factor (used to produce an import-substitute item) gain through protec­tion, even though the country as a whole loses. This is the essence of the SST which simply suggests that protection increases the real income of the scarce factor and reduces that of the abundant factor.

The SST seeks to explain the effects of international trade on income distribution .The theorem based upon the Changes in factor Prices that accompany the opening of trade .The I is fairly straightforward and may now be explained.

Let us assume that a capital-abundant country initiates trade. This will lead to an increase in the price of capital-its abundant factor, and a fall in the price of labour-its scarce factor. If we assume, in addition, that full employment exists both before and after trade, then total nominal return to capital will increase.

The reason is that the price of capital has increased but capital used remains the same. In a like manner, the total nominal return to labour will fall since the wage rate has fallen but the labour employed remains unchanged.

It is important to note, in this context, that the ability of a country to obtain goods and services depends on its real income which, in its turn, depends on changes in commodity prices, i.e., prices of exports and imports. In this case, the owners of capital who consume only the cheaper imported labour-intensive good are surely better-off, since then nominal income has increased and the price of the labour-intensive good has fallen.

Their absolute as also relative command over this product has increased. But what about those capitalists who consume only, the capital-intensive export good? This question cannot be answered easily because both their nominal income and the price of the good they consume have increased. If their income has increased faster than the price of the capital-intensive good, then their real income will in­crease. The converse is also true.

If the factor markets are competitive, then the rental rate in the capital-abundant country will increase relatively faster than the price of the export good. In equilibrium capitals rental equals the marginal product of capital (MP_K) times the price of the export good Since both the rental and the price of the export good are increasing, the nature of changes in MP_K will deter­mine which is rising faster than the other.

If capital is becoming more productive, then rental will be rising faster than the price of the export good and the real income of capital will be rising. If capital is becoming less productive, then the price of the export good will rises faster than the increase in capital rental.

As trade is opened up, the capital-abundant country will find the wage rate falling and the rental rate increasing-and its producers will respond by using relatively more labour and relatively less capital in production, i.e., the capital-labour ratio in production will fall. This will increase the productivity of capital at the margin (i.e., MP_K increases), resulting in an increase in the real income of capital.

Thus we see that the real income share of the owners of the abundant factor increases with trade. A similar argument can be used to show that the price of labour is falling faster than the price of the labour-intensive import. The reason is that with fall in the capital-labour ratio the MP_K is rising, since each unit of capital has more labour to work with. Thus, the real income of the owners of the scarce factor (labour) falls with trade.

This result-that the price of a factor changes relatively more than the price of the good inten­sive in that factor-is called the magnification effect. This follows from the hypothesis that the factor-price changes are magnified reflections of the commodity-price changes. A simple example will make the point clear. Under competition, the price of each product must equal its marginal cost.

In our car-food economy, price must equal the marginal capital and labour costs in each sector:

P_c = MC_c (marginal cost of car) = a₁r + b_1w (1) and

P_f = MC_f (marginal cost of food) = a₂r + b_2w (2)

where the product prices are measured in same units (e.g., units of a commodity, or U.S. dol­lars) r is the rental rate earned by capital and w is the wage rate paid to labour. The coefficients a₁ a₂, b₁ and b₂ are the physical input/output ratios. These indicate how much capital (a₁ and a₂) or ‘labour (b₁and b₂) is required to produce 1 unit of each good. Here we assume that these input/output coefficients are constants.

Suppose the price of car rises by 10% and the price of food remains constant. The high price of car (and the resulting expansion of car production) will bid up the return to at least one factor. In fact it is likely to raise the rental rate for capital. So, r rises. Now, let us look at eqn. (2). If r rises and the price of food remains constant, then the wage rate w has to fall in absolute terms. The fall in food production pushes the wage rate down.

Next, take the fall of w back to eqn. (1) If w is falling and P_c is rising by 10%, then r must be rising more than 10% to keep eqn. (1) valid. So, if car is capital-intensive, and w falls and P_c increase by 10% and P_f steady this means that r rises by more than 10%. Thus, a shift in relative product prices brings an even more magnified response in factor prices.

The factor used inten­sively in production of car whose price is rising after trade will have its rise even faster than the product price rise. Therefore, its real return (its purchasing power with respect to either product) rises. Labour used intensively in the production of import-competing product food will find that its real purchasing power is falling.

Thus the third aspect of the H-O theorem regarding the effects of international trade on the income distribution is stated formally by the SST.

If an economy is in full employment both before and after trade, the increase in the price of the abundant factor and the fall in the price of the scarce factor because of trade imply that the real income of the abundant factor will rise and that of the scarce factor will fall. Opening trade enables one of the factors to buy more of either good. It makes the other factor worse off in terms of its ability to buy either good.

This happens because a shift in relative product prices brings an even more magnified re­sponse in – actor prices. The factor used intensively in production in the rising-price (car) sector has its market Price (e.g., rental rate) rise even faster than the product price rise Therefore its real return (its purchasing power with respect to either product) rises. A factor used inten­sively in the other sector has its real purchasing price cut.

In our example, the lower wage rate means workers lose the purchasing power with respect to both the high-priced car and the stable-priced food. The real wage rate decreases. The result follows from the fact that price must equal marginal cost under competition-both before and after trade.

It follows, as a logi­cal corollary, that protection will have exactly the opposite effect. It will increase the return to the scarce factor and reduce the return to the abundant factor. In our example, protection will increase the price of food, and keep the price of car unchanged. So real wage rate rises and real rental rate falls.

Theory and Reality:

The SST has an important practical implication. It provides some support for the cheap foreign labour argument for protection. For example, in the USA, unskilled labour has an incentive to seek protection against imports of commodities that are relatively intensive in unskilled labour in reality, relative factor prices do not respond to trade as much as the H-O model predicts’.

Furthermore, personal (household) distribution of income reflects not only the distribution of income between factors of production. Most individuals or families own more than one factor of production. For this reason, the final impact of trade on personal distribution of income is not quite transparent.

Relation with H-O Theorem:

It has to be noted that the proof of the SST does not depend on the validity of the H-O theorem or the factor price equalisation theorem. The reason is easy to find out. The SST does not involve any comparison between countries. The theorem will hold even in the presence of factor intensity reversals and drastic differences in production functions and tastes between countries.