In this article we will discuss about the Marginal Rate of Technical Substitution (MRTS) between Two Variable Inputs.
Let us suppose that the firm uses two variable inputs X and Y and the firm’s production function is
q = f(x, y) [eq (8.21)]
Let us also suppose that it is possible for the firm to substitute one of the inputs for the other. Now, at any particular point on an isoquant (IQ), if the firm uses one additional (or marginal) unit of input X, then the quantity by which the use of input Y can be reduced so that the firm’s output may remain the same, i.e., it may remain on the same IQ, is called the marginal rate of technical substitution of the input X for the input Y (MRTSX,Y).
MRTSX, Y the Numerical Slope of an IQ:
ADVERTISEMENTS:
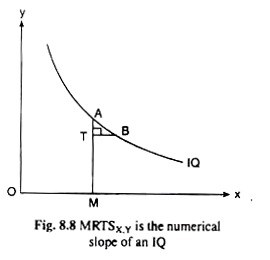
As said above, the MRTS is defined at a point on an IQ. We may explain the economic significance of MRTS with the help of Fig. 8.8. Here the isoquant is given by the curve IQ. Let us suppose that the firm can produce q units (= constant) of its output at any point on this curve.
Therefore, at any particular point A on IQ, the firm uses the quantities OM and AM of the inputs X and Y and produces q units of its product. Now, if the firm uses TB (units) more of X, then, in order to produce the same quantity of output, i.e., in order to remain on the same IQ, it would use AT units less of Y.
Therefore, at the point A, if the firm uses one additional unit of X, it would have to use AT/TB less of Y, i.e., at the point A on IQ, the marginal rate of technical substitution of X for Y is AT/TB which is the numerical value of the slope of the isoquant, IQ, at the point A, provided TB is infinitesimally small. We have obtained, therefore, MRTSX,Y = numerical slope of the isoquant.
MRTSX,Y the Ratio of MPX and MPY:
ADVERTISEMENTS:
The curve IQ in Fig. 8.8 is a particular isoquant of the firm and the points A and B are any two very close y points on this curve. The numerical value of the slope of the isoquant or MRTSX,Y at the point A is AT/TB. If the firm moves along the IQ from the point A to the point B, then he would use AT less of Y and TB more of X.
Now, as the firm uses AT less of Y, its output would fall by AT.MPY [since MPY is the increase or decrease in output due to an increase or decrease in the use of input Y by an additional, or, marginal unit].
On the other hand, as the firm increases the use of X by TB, its output would increase by TB. MPX [since MPX is the increase in output due to the increase in the use of X by an additional unit]. Now, the firm’s output would remain unchanged as it moves along the IQ from the point A to the point B.
ADVERTISEMENTS:
That is why we may write: