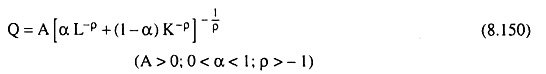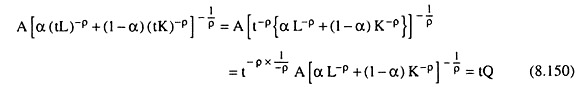A production function with constant elasticity of substitution (CES) between the inputs—the CES production function as it is called—has two major characteristics. First, it is homogeneous of degree one. Second, it has a constant elasticity of substitution. Production functions which do not possess one or both of these characteristics do not belong to the CES class.
The Cobb-Douglas (C-D) production function Q = ALαKβ, has CES = 1. Thus, all C-D production functions possess the second characteristic. However, the first criterion is satisfied only for α + β = 1. The production function Q = ALαK1-α + L is homogeneous of degree one, but does not have a CES. It, therefore, does not belong to the CES class. The equation of the CES production function is
where L and K represent two factors of production, and A, α and ρ are three parameters. The parameter A (the efficiency parameter) plays the same role as the coefficient A in the Cobb-Douglas production function; it serves as an indicator of the state of technology.
ADVERTISEMENTS:
The parameter α, like the α in the C-D function has to do with the relative factor shares in the product. Lastly, the parameter ρ is the substitution parameter. It has no counterpart in the C-D function. The parameter ρ determines the value of the (constant) elasticity of substitution.
Let us first note that the CES function (8.150) is homogeneous of degree one, because if we change L and K by the factor t where t is a positive real number, then output Q will change to
Consequently, the CES function, like all linearly homogeneous functions, would give us constant returns to scale (CRS), and it would possess all the general properties of CRS or HPF (homothetic production function) of degree one.
ADVERTISEMENTS:
We may also note that the isoquants (IQs) generated by the CES production function are always negatively sloped and strictly convex for positive values of L and K. In order to establish this, let us first obtain the expressions for the marginal products of the inputs. Now using the notation [*] for the expression [a Lρ + (1 – α) K-ρ], we have
We may now proceed to obtain the coefficient of elasticity of substitution (σ) under the CES. The condition for cost minimisation subject to an output constraint is