A consumer is said to be in equilibrium when he is buying such a combination of goods as leaves him with no tendency to rearrange his purchases of goods.
He is then in a position of balance in regard to the allocation of his money expenditure among various goods.
In the indifference curve technique the consumer’s equilibrium is discussed in respect of the purchases of two goods by the consumer.
As in the cardinal utility analysis, in the indifference curve analysis also it is assumed that the consumer tries to maximise his satisfaction. In other words, the consumer is assumed to be rational in the sense that he aims at maximising his satisfaction.
ADVERTISEMENTS:
Besides, we shall make the following assumptions to explain the equilibrium of the consumer:
(1) The consumer has a given indifference map exhibiting his scale of preferences for various combinations of two goods, X and Y.
(2) He has a fixed amount of money to spend on the two goods. He has to spend whole of his given money on the two goods.
(3) Prices of the goods are given and constant for him. He cannot influence the prices of the goods by buying more or less of them.
ADVERTISEMENTS:
(4) Goods are homogeneous and divisible.
To show which combination of two goods, X and Y, the consumer will decide to buy and will be in equilibrium position, his indifference map and budget line are brought together.While indifference map portrays consumer’s scale of preferences between various possible combinations of two goods, the budget line shows the various combinations which he can afford to buy with his given money income and given prices of the two goods. Consider Fig. 8.19 in which we depict consumer’s indifference map together with the budget line BL.
Good X is measured on the X-axis and good Y is measured on the X-axis. With a given money to be spent and given prices of the two goods, the consumer can buy any combination of the goods which lies on the budget line BL. Every combination on the budget line BL costs him the same amount of money. In order to maximise his satisfaction the consumer will try to reach the highest possible indifference curve which he could with a given expenditure of money and given prices of the two goods. Budget constraint forces the consumer to remain on the given budget line, that is, to choose a combination from among only those which lie on the given budget line.
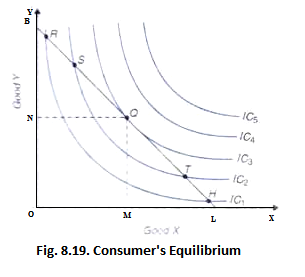
It will be seen from Fig. 8.19 that the various combinations of the two goods lying on the budget line BL and which therefore the consumer can afford to buy do not lie on the same indifference curve; they lie on different indifference curves. The consumer will choose that combination on the budget line BL which lies on the highest possible indifference curve.
ADVERTISEMENTS:
The highest indifference curve to which the consumer can reach is the indifference curve to which the budget line BL is tangent. Any other possible combination of the two goods either would lie on a lower indifference curve and thus yield less satisfaction or would be unattainable.
In Fig. 8.19 budget line BL is tangent to indifference curve IC3 at point Q. Since indifference curves are convex to the origin, all other points on the budget line BL, above or below the point Q, would lie on lower indifference curves. Take point R which also lies on the budget line BL and which the consumer can afford to buy. Combination of goods represented by R costs him the same as the combination Q. But, as is evident, R lies on the lower indifference curve IC1 and will therefore yield less satisfaction than Q.
Likewise, point S also lies on the budget line BL but will be rejected in favour of Q since S lies on the indifference curve IC2 which is also lower than IC3 on which Q lies. Similarly, Q will be preferred to all other points on the budget line BL which lies to the right of Q on the budget line, such as T and H.
It is thus clear that of all possible combinations lying on budget line BL, combination Q lies on the highest possible indifference curve IC3 which yields the consumer maximum possible satisfaction. Of course, combinations lying on indifference curves IC4 and IC5 will give greater satisfaction to the consumer than Q, but they are unattainable with the given money income and the given prices of the goods as represented by the budget line BL.
It is therefore concluded that with the given money expenditure and the given prices of the goods as shown by BL the consumer will obtain maximum possible satisfaction and will therefore be in equilibrium position at point Q at which the budget line BL is tangent to the indifference curve IC3. In this equilibrium position at Q the consumer will buy OM amount of good X and ON amount of good Y.
At the tangency point Q, the slopes of the budget line BL and indifference curve IC3 are equal. Slope of the indifference curve shows the marginal rate of substitution of X for Y (MRSxy), while the slope of the budget line indicates the ratio between the prices of two goods Px/Py. Thus, at the equilibrium point Q.
MRSxy = Price of good X/ Price of good Y = Px/Py
When the marginal rate of substitution of X for Y (MRSxy) is greater or less than the price ratio between the two goods, it is advantageous for the consumer to substitute one good for the other. Thus, at points R and S in Fig. 8.19, marginal rates of substitution (MRSxy) are greater than the given price ratio, the consumer will substitute good X for good Y and will move down along the budget line BL .He will continue to do so until the marginal rate of substitution becomes equal to the price ratio, that is, the given budget line BL becomes tangent to an indifference curve.
On the contrary, marginal rates of substitution at points H and Tin Fig. 8.19 are less than the given price ratio. Therefore, it will be to the advantage of the consumer to substitute good y for good X and accordingly move up the budget line BL until the MRSxy rises so as to become equal to the given price ratio.
ADVERTISEMENTS:
We can therefore express the condition for the equilibrium of the consumer by either saying that the given budget line must be tangent to the indifference curve, or the marginal rate of substitution of good X for good Y must be equal to the ratio between the prices of the two goods.
Second Order Condition for Consumer Equilibrium:
The tangency between the given budget line and an indifference curve or, in other words ‘the equality between MRSxy and the price ratio is a necessary but not a sufficient condition of consumer’s equilibrium. The second order condition must also be fulfilled. The second order condition is that at the point of equilibrium indifference curve must be convex to the origin, or to put it in another way, the marginal rate of substitution of X for Y must be falling at the point of equilibrium.
It will be noticed from Fig. 8.19 above that the indifference curve IC3 is convex to the origin at Q, Thus at point Q both conditions of equilibrium are satisfied. Point Q in Fig. 8.19 is the optimum or best choice for the consumer and he will therefore be in stable equilibrium at Q.
ADVERTISEMENTS:
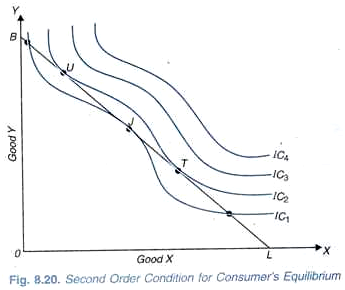
But it may happen that while budget line is tangent to an indifference curve at a point but the indifference curve may be concave at that point. Take for instance, Fig. 8.20 where indifference curve IC1 is concave to the origin around the point J. Budget line BL is tangent to the indifference curve IC1 at point J and MRSxy is equal to the price ratio, Px/Py.
But J cannot be a position of equilibrium because consumer’s satisfaction would not be maximum there Indifference curve IC1 being concave at the tangency point J, there may be some points on the given budget line BL such as U and T, which will lie on an indifference curve higher than IC1. Thus the consumer by moving along the given budget line BL can go to points such as U and T and obtain greater satisfaction than at J.
We therefore conclude that for the consumer to be in equilibrium, the following two conditions are required:
ADVERTISEMENTS:
1. A given budget line must be tangent to an indifference curve, or marginal rate of substitution of X for Y (MRSxy) must be equal to the price ratio of the two goods Px/Py
2. Indifference curve must be convex to the origin at the point of tangency.
The above explanation of consumer’s equilibrium in regard to the allocation of his money expenditure on the purchases of two goods has been made entirely in terms of the consumer’s relative preferences of the various combinations of two goods. In this indifference curve analysis of consumer’s equilibrium no use of cardinal utility concept has been made which implies that satisfaction or utility obtained from the goods is measurable in the quantitative sense.