The following points highlight the two main conditions of Pareto optimality. The conditions are: 1. Efficiency in Exchange 2. Efficiency in Production.
1. Efficiency in Exchange:
The first condition for Pareto optimality relates to efficiency in exchange. The required condition is that “the marginal rate of substitution between any two products must be the same for every individual who consumes both.”
It means that the marginal rate of substitution (MRS) between two consumer goods must be equal to the ratio of their prices. Since under perfect competition every consumer aims at maximising his utility, he will equate his MRS for two goods, X and Y to their price ratio (Px/Py).
Suppose there are two consumers A and В who buy two goods X and Y, and each faces the price ratio Px/Py… Thus A will choose X and Y such that his AMRSxv = Xx/Py. Similarly В will choose X and Y such that his MRSXY =Px/Py. Therefore, the condition for efficiency in exchange is AMRSxv = BMRSxv –Px/Py.
ADVERTISEMENTS:
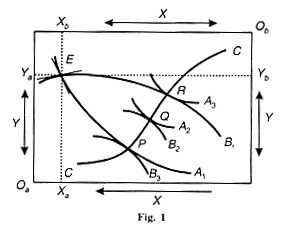
The box diagram Figure 1 explains the optimum condition of exchange. Take two individuals A and В who possess two goods X and Y in fixed quantities respectively. Oa is the origin for consumer A and Ob the origin for В (turn the diagram upside down for its understanding).
The vertical sides of the two axes, Oa and Ob, represent good Y and the horizontal sides, good X. The indifference map of A is represented by A the curves A1 A2 and A3 and B’s map by B1 B2and B3 indifference curves.
Any point within this box represents a possible distribution of the two goods between the two individuals. Take point E where the two indifference curves A 1 and B1 intersect. At this position, A possesses OaYa units of Y and OaXa of good X. В receives ObYb of Y and Ob Xb of X.
At point E the marginal rate of substitution between the two goods is not equal to the ratio of their prices because the two curves do not have the same slope. So E is not the point of у optimum exchange of the two goods X and Y between the two individuals A and B. Let us try to find out such a point where one individual becomes better off without making the other worse off.
ADVERTISEMENTS:
Suppose A would like to have more of X and В more of Y. Each will be better off without making the other worse off if he moves to a higher indifference curve. Let them move from point E to R. At R, A gets more of Х by sacrificing some Y, while В gets more of Y by sacrificing some amount of X.
There is no improvement in B’s position because he is on the same indifference curve B1 but A is much better off at R having moved to a higher indifference curve from A1 to A3 If, however, A and В move from E to P, A is as well off as before for he remains on the same indifference curve A1 В becomes much better off having moved from B1 to B3.
It is only when they move from E to Q that both are on higher indifference curves. P, Q and R are, thus, the three conceivable points of exchange, The contract curve CC is the locus of these points of tangency which shows the various positions of exchange that equalize the marginal rates of substitution of X and Y.
ADVERTISEMENTS:
Any point on the CC curve, therefore, satisfies this optimum condition of exchange. But a movement along the contract curve in either direction always tends to make one individual better off at the expense of the other. Thus each point on the contract curve represents optimum social welfare in the Paretian sense.
2. Efficiency in Production:
The second condition for Pareto optimality relates to efficiency in production. There are three allocation rules for demonstrating efficiency in production under perfect competition. Rule one relates to the optimum allocation of factors. It requires that the marginal rate of technical substitution (MRTS) between any two factors must be the same for any two firms using these factors to produce the same product.
Suppose there are two firms A and В that use two factors: labour (L) and capital (K) and produce one product. Given the prices of the two factors, a firm is in equilibrium under perfect competition when the slope of an isoquant equals the slope of the iso-cost line.
The slope of an isoquant is the MRTS of labour and capital, and the slope of the iso-cost line is the ratio of the prices of labour and capital. Thus the condition of equilibrium for firm A is AMRTSLK. = PL/PK, and that of firm В is BMRTSLK, = PLPK. Therefore, rule one for efficiency in production is AMRTSLK = BMRTSLK= PL/PK.
Rule two states that the marginal rate of transformation between any factor and any product must be the same for any pair of firms using the factor and producing the product. It means that the marginal productivity of any factor in producing a particular product must be the same for all firms.
A firm under perfect competition will employ a factor of production up to the point at which its marginal value product (VMP) equals it price. If MPP is the marginal physical product of factor L (labour) in the production of good X in firm A, then its VMP is the marginal physical productivity multiplied by the price of X, that is VMP = A MPPXL;. PX Thus the price of labour (PL) in firm A is
PL = A MPPXL. PX or PL/PX, = AMPPXL … (1)
Similarly, in firm В the price of labour is
PL = BMPPXL. P, or PJPX = BMPPXL … (2)
ADVERTISEMENTS:
Since the price of the product (Px) and the price of labour (P,) are the same in both the firms, each firm will equate its marginal physical productivity to PL/ PX Thus from equations (1) and (2), we have
АМРРXL = BMPP = PL/Px.
Thus in equilibrium each firm has the same marginal physical productivity of factor L in producing the same product X. Rule three for efficiency in production requires that the marginal rate of transformation (MRT) between any two products must be the same for any two firms that produce both. This condition requires that if there are two firms A and B, and both produce two products X and Y, then AMRTXY = BMRTXY
A profit maximising firm under perfect competition will be in equilibrium when the iso-revenue line is tangent to its transformation curve. It means that for equilibrium the marginal rate of transformation between two products X and Y must equal their price ratio, i.e., MRTXY= PX/Py . Thus the optimum condition in the case of firm A will be BMRTXY, = PX/Py. And in the case of the firm В it will be BMRTXY= PXPY Thus, AMRTXY, = BMRTXY = PXPY.
ADVERTISEMENTS:
This rule is explained in terms of Figure 2. The MRT between any two products is the rate at which one product would have to be sacrificed in order to produce more of the other product with the same quantity of resources. It is measured on the diagram by the slope of the transformation curve PP1 at any point. TR is the iso-revenue line whose slope 1 shows PXPY. At point E the slopes of the transformation curve PP1 and the iso revenue line TR are equal so that MRTXY, = PXPY Thus each firm maximises its output by producing and selling OX1 of commodity X and OY1 of commodity Y.
In fact, the MRT of X for Y is equal to the ratio of the marginal cost of product X (MCX) to that of product Y (MCX). But each firm produces that level of output at which its marginal cost is equal to its market price. Therefore, for each firm Px = MCX and Py = MCY Hence MCX/MCY = PX/Py.
Efficiency in Exchange and Production (Product Mix):
Pareto optimality under perfect competition also requires that the marginal rate of substitution (MRS) between two products must equal the marginal rate of transformation (MRT) between them. It means simultaneous efficiency in consumption and production.
ADVERTISEMENTS:
Since the price ratios of the two products to consumers and firms are the same under perfect competition, the MRS of all individuals will be identical with MRT of all firms consequently, the two products will be produced and exchanged efficiently. Symbolically, MRSXY = PX/PY, and MRTxy = Px/Py. Therefore, MRSXY = MRTxy.
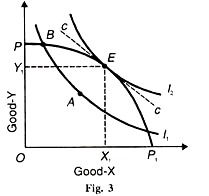
Figure 3 illustrates overall Pareto optimality in consumption and production. PP; is the transformation curve or the production possibility frontier for two goods X and Y. Any point on the PP curve shows the marginal rate of transformation (MRT) between X and Y which reflects the relative opportunity costs of producing X and Y, that is MCx/MCy . Curves I1 and I2 are the indifference curves which represent consumer tastes for these two goods.
The slope of an indifference curve at any point shows the marginal rate of substitution (MRS) between X and Y. Pareto optimality is achieved at point E where the slopes of the transformation curve PPt and the indifference curve 12 are equal. This equality in slopes is shown by the price line cc which indicates that at point £ the MRSxy = MRTxy = Px/Py or MUx/MUy_=MCx/MCr = Px/Py.
Given the production possibility frontier PP1, there is no other indifference curve which satisfies Parteo efficiency. Point A is of inefficient production because it is below the PPI curve. Point B is on the production possibility frontier but it is on a lower indifference curve I1, where the consumer satisfaction is not maximised. Therefore, Pareto optimality exists only at point E, where there is efficiency in both consumption and production when the society consumes and produces OX1 of good X and OY1 of good Y.
Thus the conditions necessary for the attainment of Pareto optimality relate to efficiency in consumption, efficiency in production, and efficiency in both consumption and production.
ADVERTISEMENTS:
These Pareto optimality conditions will be achieved if:
(1) second-order conditions are satisfied for each consumer and producer,
(2) No consumer is satiated,
(3) There are no external effects either in consumption or production,
(4) There are no indivisibilities, and
(5) There are no imperfections in factor and product markets.