Learn about the comparison between Pareto optimality and welfare optimality.
The Pareto optimality is necessary but not sufficient for welfare maximisation. We have seen that welfare maximisation occurs at some point on the GUPF where the GUPF is a tangent to an SIC.
Therefore, since every point on the GUPF satisfies all the three conditions of Pareto optimality, Pareto optimality is necessary for welfare maximisation. But any point on the GUPF—although Pareto-optimal—is not the point of maximum welfare; only the point of tangency is. That is why Pareto optimality is not sufficient for welfare maximisation.
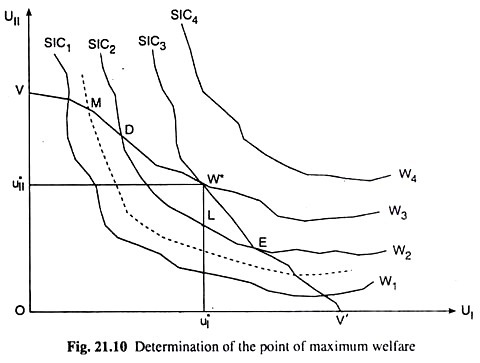
We may note here another interesting point. A Pareto-non-optimal point may indicate a higher level of utility than a Pareto-optimal point. For example, in Fig. 21.10, the point M lies on the GUPF. So it is a Pareto-optimal point.
On the other hand, the point L, although lying on a higher SIC (than M) i.e., although indicating a higher level of W, is located below the GUPF giving us that it is Pareto-non-optimal.
However, it can be shown that, given any inefficient point like L that lies below the GUPF, we can obtain some point(s) like the point D or E on the same SIC as L that takes us on a higher SIC than that of M and also on the GUPF, i.e., the point like D or E takes us to an improved situation than M and on an efficient situation like M.