Efficiency in Output Markets (With Diagram)!
When output markets are perfectly competitive, all consumers allocate their budgets so that their MRS between two goods are equal to the price ratio.
That is: MRS = PX /PY. At the same time, each profit-maximising firm will produce its output up to the point where price is equal to marginal cost. That is: PX = MCX and PY = MCY because the MRT = MCX/MCY = PX/PY = MRS ……….(5)
When both output and input markets are competitive, the production of two goods will be efficient in that the MRT = MRS. This condition is just the marginal benefit and marginal cost rule discussed under demand curves where we saw that consumers buy additional units of a good to the point at which MB of consumption = MC.
ADVERTISEMENTS:
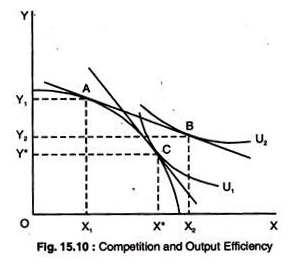
Here the production of two goods is chosen so that the MB of consuming another unit of X = MC of producing X, and the same is true for the consumption and production of Y’. Fig. 15.10 shows that efficient competitive output markets are achieved when production and consumption choices are separated.
Suppose the market generates a price ratio P’X/P’Y. If producers are using inputs efficiently, they will produce two products at A, where the price ratio is equal to the MRT, the slope of the PPF.
When faced with the budget constraint, consumers will consume at B, where they maximise their utility at U2. But if the producer wants to produce X units of X and consumers wish to consume X2, there will be an excess demand for X.
Correspondingly, as consumers wish to consume Y2 units of Y, but producers want to sell Yi units, there will be excess supply of Y. Prices will then adjust—the price of X will rise and that of Y will fall. As PX/PY increases, the price line will move along the production frontier.
An equilibrium will be established at P*X/P*Y at C, where producers want to sell X* units of X and Y* units of Y, and consumers wish to buy the same amounts. At this equilibrium, the MRT = the MRS, so, again, the competitive equilibrium is efficient.