Equity and Efficiency of Exchange (With Diagram)

In this article we will discuss about the equity and efficiency of exchange.

Pareto efficiency of exchange in the two-consumer, two-good model, we have seen that many different efficient allocations of the given quantities of the two goods are possible, and we have seen how a perfectly competitive economy generates an efficient allocation. But some allocations are likely to be more fair or equitable than others.

Of course, the economists disagree about how to define equity and how to quantify it. For, the question involves subjective comparisons of utility. In order to elaborate the point, let us remember that the points on the contract curve of exchange (CCE) in Fig. 21.2 shows the levels of utility that the two individuals can achieve.

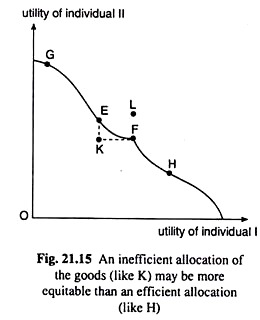
In Fig. 21.15 we put the information from the Edge-worth box in a different form. Here individual I’s utility is measured on the horizontal axis and II’s on the vertical axis. There is a one-to-one correspondence between the points in the Edge-worth box and those in Fig. 21.15, because every allocation generates a utility combination of the two individuals.

Let us also remember that the utility possibility frontier in Fig. 21.15 represents all allocations that are efficient, because the UPF is made up of the points on the CCE. There is a one-to-one correspondence between the points on the CCE and those on the UPF. As we move upward towards right along the CCE, utility of individual I increases and that of II decreases.

That is why the slope of the UPF is negative. Let us suppose that the points G, E, F and H on the UPF in Fig. 21.15 correspond, respectively, to the points G,E,F and H on the CCE in Fig. 21.2. Since the points G, E, F and H lie on the CCE, one person cannot be made better off without making the other worse off if we move from any one of the points to another.

Therefore, all these points and their corresponding points on the UPF represent Pareto- efficient distribution of the goods. Any point like K below the UPF in Fig. 21.15, however, represents an inefficient allocation because by means of further redistributions of the goods, the economy may reach a point on the EF segment of the UPF, which would signify an increase in the utility level of at least one individual without reducing that of the other.

Also, at any point like L, above the UPF, both the individuals would be better off as compared to some point(s) on the UPF, but such a point is unattainable because the higher levels of utility for both the parties, generated by such a point, would require larger quantities of the goods than what are given to us.

In the above analysis, we see that the points on the EF segment of the UPF are more efficient than K, for each makes at least one person better off without making the other worse off. We may conclude, therefore, that an allocation must be efficient (i.e., must lie on the CCE or the UPF) to be equitable.

But, let us suppose, K and H in Fig. 21.15 are the only possible allocations. Then, we can say, not necessarily, that H is more efficient than K. Compared with K, H yields more utility for individual I and less for individual II.

Now some people who think that ‘I should get a more fair deal’, would say that H is more equitable than K, and some other people who think the opposite would say that K is more equitable than H. We may conclude, therefore, that one inefficient allocation of the goods (i.e., one lying below the UPF) may be more equitable than another efficient allocation (i.e., one lying on the UPF).

The problem, therefore, is how to define an equitable allocation. Even, of all the points on the UPF, we may ask which is the most equitable. The answer involves interpersonal comparisons of utility, and this takes us to the social welfare functions.

We often use a social welfare function (SWF) to describe the particular weights that are applied to each individual’s utility in determining what is socially desirable. For example, one SWF, viz., the utilitarian, weights everyone’s utility equally and, consequently, maximises the total utility of all members of society. Each SWF can be associated with a particular view about equity.

But some views do not explicitly weight individual utilities and cannot therefore be represented by SWF. For example, a market-oriented view argues that the outcome of the competitive market process is equitable because it rewards those who are most able and work the hardest, although this outcome may give rise to a less equal allocation of goods.

On the other hand, the Rawlsian view emphasises that an equal distribution of resources may remove the incentives that induce the most productive people to work hard because their wealth will be taxed away. This view allows inequalities if they make the least well-off person in society better off. According to Rawls, the most equitable allocation maximises the utility of the least well-off person in society.

We have listed the four views of equity in Table 21.1. They move roughly from the most to the least egalitarian. The egalitarian view explicitly requires equal allocations, while the Rawlsian puts a heavy weight on equality; otherwise, some would be much worse off than others.

The utilitarian is likely to require some difference between the best and worse-off members of society. Finally, the market-oriented view may lead to substantial inequality in the allocations of goods and services.

Equity and Perfect Competition:

We have obtained that a competitive equilibrium leads to a Pareto-efficient outcome that may or may not be equitable. Since efficient allocations are not necessarily equitable, society must rely, to some extent, on the government to achieve equity goals by redistributing income or goods among households. These goals can be reached through the tax system.

The government can also provide public services, such as medical aid, to the poor, or it can transfer funds through such programmes as food stamps. Unfortunately, all programmes that redistribute income in our society are economically costly. Taxes may encourage individuals to work less or cause firms to devote resources to avoiding taxes rather than to producing output.

So, in effect, there is a trade-off between the goals of equity and efficiency, and hard choices must be made. Welfare economics provides a useful framework for debating the normative issues that surround the equity-efficiency issue in public policy.