Let us make an in-depth study of the general equilibrium between exchange and production.
General equilibrium in exchange must be consistent with general equilibrium in production to have a general equilibrium within the economy.
This means that we need to derive a transformation curve (or ppc) which is a reflection of the contract curve in the box diagram depicting general equilibrium of production. Thus, the transformation curve gives all possible equilibrium combinations of goods X and F that could be produced by employing all available inputs.
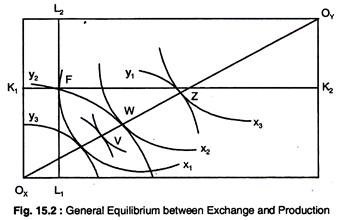
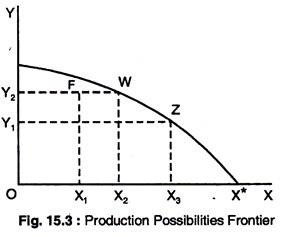
Although this gives the same information as is given by the contract curve, it is plotted on a graph with the axis representing curve which is derived from Fig. 15.2. Point W on the contract curve in Fig. 15.2 depicts tangency of isoquants x2 and y2, which represent the production of x2 of X and y2 of Y.
These quantities are plotted as point Won the transformation curve in Fig. 15.3. Similarly, point Z is drawn in Fig. 15.3. For every point on the contract curve in Fig. 15.2, there is a corresponding point on the transformation curve in Fig. 15.3. If good Y is not produced, then the maximum amount of X, X*, can be produced, which corresponds to the origin Y; OY in Fig. 15.2.
If we select a point that is not on the contract curve, such as point F in Fig. 15.2, we see that this translates into a point that is not on the transformation curve, e.g. point Fin Fig. 15.3. We can see that point F could not represent a general equilibrium in production since the economy is capable of producing more of X without reducing the output of Y by moving to point W.
Finally, the slope of the transformation curve is called the marginal rate of transformation (MRT).
The condition necessary for general equilibrium between exchange and production is MRS = MRT. General equilibrium in exchange occurs when both individuals have the same MRS, which is a point on the contract curve. When the MRS = the MRT, there is a general equilibrium between exchange and production.
ADVERTISEMENTS:
An example will clarify this position. Suppose, the MRS is 1X: 1Y, that is, each individual will stay at the same level of satisfaction if one unit of X is exchanged for one unit of Y. Now, suppose the MRT is 1X: 3Y, that is, by producing one unit less of X, 3 units of Y can be produced. Thus, MRS ≠MRT = MCX/MCY.
Under the circumstances, the level of satisfaction of one or both individuals could be increased through a change in production. For example, if 1 unit of X has to be given to produce 3 more units of Y. But either individual is willing to give up 1 unit of X for 1 unit of Y.
Since production will bring forth 3 units of Y at a cost of 1 unit of X, then either individual will be at the same level of satisfaction by receiving 1 unit of Y for 1 unit of X, and there will still be 2 additional units of Y left over. These 2 units of Y can be used to increase the level of satisfaction of either individual or of both individuals. Thus, more of Y and less of X will be produced until MRT = MRS.