Bain’s Models for Limit-Pricing Theory of Markets

Bain formulated his ‘limit-price’ theory in an article published in 1949, several years before his major work Barriers to New Competition which was published in 1956.

His aim in his early article was to explain why firms over a long period of time were keeping their price at a level of demand where the elasticity was below unity, that is, they did not charge the price which would maximize their revenue.

His conclusion was that the traditional theory was unable to explain this empirical fact due to the omission from the pricing decision of an important factor, namely the threat of potential entry. Traditional theory was concerned only with actual entry, which resulted in the long-run equilibrium of the firm and the industry (where P = LAC).

However, the price, Bain argued, did not fall to the level of LAC in the long run because of the existence of barriers to entry, while at the same time price was not set at the level compatible with profit maximization because of the threat of potential entry. Actually he maintained that price was set at a level above the LAC (= pure competition price) and below the monopoly price (the price where MC = MR and short-run profits are maximized).

This behaviour can be explained by assuming that there are barriers to entry, and that the existing firms do not set the monopoly price but the ‘limit price’, that is, the highest price which the established firms believe they can charge without inducing entry. Bain, in his 1949 article, develops two models of price setting in oligopolistic markets.

Assumptions:

1. There is a determinate long-run demand curve for industry output, which is unaffected by price adjustments of sellers or by entry. Hence the market marginal revenue curve is determinate. The long-run industry-demand curve shows the expected sales at different prices maintained over long periods.

2. There is effective collusion among the established oligopolists.

3. The established firms can compute a limit price, below which entry will not occur.

The level at which the limit price will be set depends:

(a) On the estimation of costs of the potential entrant,

(b) On the market elasticity of demand

(c) On the shape and level of the LAC,

(d) On the size of the market,

(e) On the number of firms in the industry.

4. Above the limit price, entry is attracted and there is considerable uncertainty concerning the sales of the established firms (post entry).

5. The established firms seek the maximization of their own long-run profit.

Model A: there is no collusion with the new entrant:

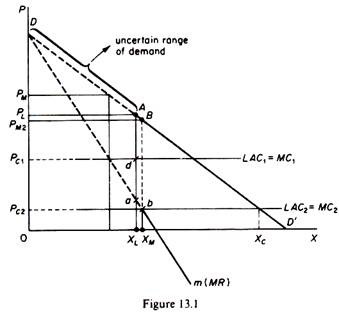
Assume that the market demand is DABD’ and the corresponding marginal revenue is Dabm (figure 13.1).

Assume further that the limit price (P_L) is correctly calculated (and known both to the existing firms and to the potential entrants). Given P_L, only the part AD’ of the demand curve and the section am of the MR are certain for the firms. The part to the left of A, that is, DA is uncertain, because the behaviour of the entrant is not known.

Whether the firms will charge the P_L or not depends on the profitability of alternatives open to them, given their costs.

Assume the LAC (which is uniquely determined by the addition of the LMC = LAC of the collusive oligopolists) is LAC₁. In this case two alternatives are possible.

Either to charge the P_L (and realise the profit P_LAdP_c1 with certainty).

Or to charge the monopoly price, that is, the price that corresponds to the intersection of LAC₁ = MC₁ with the MR. This price will be higher than P_L (given LAC₁), but its precise level is uncertain post-entry. Thus the profits in the second alternative are uncertain and must be risk-discounted. The firm will compare the certain profits from charging P_L with the heavily risk-discounted profits from the second ‘gamble’ alternative, and will choose the price (P_L or P_M) that yields the greatest total profits.

Assume that the LAC is LAC₂ = MC₂. In this case the price that maximises profit is P_M2 (corresponding to the intersection MC₂ and MR over the certain range of the latter). The P_M2 is lower than P_L. The firm will clearly charge P_M2 which maximises the profits. In this case the ceiling set by the price P_L is not operative.

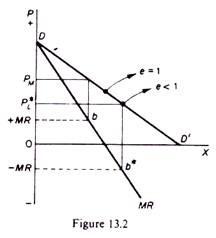
The observed fact of setting the price at a level where e < 1 is justified by a situation where the limit price is low, cutting the demand curve at a point at which the MR is negative (figure 13.2). Clearly if the limit price is P_L* the MR is b* which is negative and hence the elasticity of demand at price P_L is less than unity.

In summary: given that an entry-preventing price P_L is defined, the alternatives open to the established firms are three:

1. To charge a price equal to P_L and prevent entry.

2. To charge a price below P_L and prevent entry (this will be adopted if P_M < P_L).

3. To charge a price above P_L and take the risks associated with the ensuing entry and the indeterminate situation that arises in the post-entry period. (This course of action will be in any case adopted if P_L < LAC).

The firm will choose the alternative which maximises profit.

Model B: collusion takes place with the new entrant:

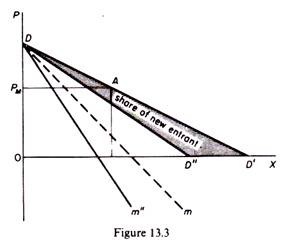
With collusion assumed to take place between the established firms and the entrant the conclusions are as before. The model is easier, however. With collusion the whole D curve shifts to the left by the share which is allocated to the new entrant at each price. The new DD” curve is known with certainty at all its points, as a consequence of the collusion, and so is the corresponding m” (figure 13.3).

Again the alternatives open to the firm are three:

1. Either charge P_L and exploit AD’ without entry.

2. Or charge a price above P_L and attract entry. The firm will eventually move to a point on the share-of-the-market curve DD”, via collusive agreement with the new entrant.

3. Or charge the profit-maximizing price P_M, if P_M < P_L.

Among these alternatives the firm will choose the one that yields maximum profits.

The basic and crucial assumptions of the above analysis are firstly, that the entrants react on the basis of the current price they expect the price charged by the established firms to continue in the post-entry period; secondly, that the established firms are aware of the threat of potential entry; thirdly, that the established firms can estimate correctly the limit price.

Then three major possibilities exist:

The policy of pricing to maximize industry profit with no entry resulting is adopted when P_L > P_M, i.e. the limit price is not operative because by charging the lower P_M price (monopoly price corresponding to MC = MR) profits (certain in this case) are maximized.

Pricing to forestall entry with industry profits not maximized, but the profit of established sellers maximized, is adopted when P_L < P_M and the certain profit accruing by charging P_L is greater than the heavily risk-discounted profit which would accrue if the higher P_M were charged and an uncertain quantity sold.

Pricing to maximize industry profit but with resulting entry. This implies P_M > P_L. This action would be chosen if it is more profitable as compared with charging P_L and necessarily, if P_L < LAC.

The first two situations lead to long-run equilibrium of the industry without entry or exit. The third case implies an unstable equilibrium since entry would be taking place.

In all the above cases one should add to the profits of established sellers any trans­itional profit which the established sellers might gain while raising the price above P_L and before entry became effective.

The new element of Bain’s model is the redrawing of the market demand so as to account for the threat of entry. Once the demand is redefined, the model accepts collusion and profit maximisation as valid hypotheses, capable of explaining the policy of setting a price below the monopoly level, that is, below the level that maximises profit. Bain’s model is not incompatible with profit maximisation.

The limit price will be chosen in favour of monopoly price if the former yields maximum long-run profits. The rationale of adopting an entry-prevention policy is profit maximisation. Whenever such a limit price is adopted it is implied that the firm has done all the relevant calculations of profits of alternative policies and has adopted the limit price because this yields maximum profits.