Production Function: Meaning and Types

In this article we will discuss about the meaning and types of production function.

Meaning of Production Function:

Production is a process whereby some goods and services, called inputs are transformed into other goods and services called output. The production function refers to the relationship between the input of factor services and the output of the resultant product. The production function is based on the idea that the amount of output in a production process depends upon the amount of inputs used in the process.

Output depends upon an input or a set of inputs in such a way that there is one unique amount of output resulting from each set of inputs. This unique relationship between output and inputs is termed as production function.

Halcrow defines production function as follows:

“Production function is the technical relationship between inputs & output indicating the amount of output that can be produced with each and every set or combination of the specified inputs”. A production function always assumes as given, a state of knowledge and technology.

A production function may be expressed in three forms:

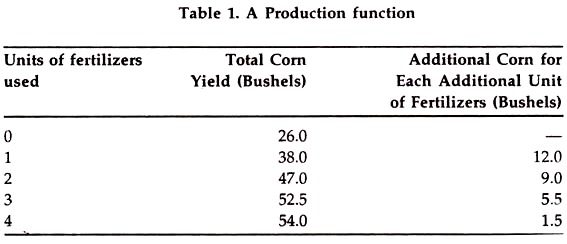
(a) It can be expressed in the form of an arithmetic table where first few columns show the input of the factors and the last column shows total output of the product as has been depicted below. Here, for the sake of simplicity, we take only one input.)

In the above table, fertilizer is the variable input (applied to a fixed price of land with other fixed inputs). Total corn yield is increasing (column 2) as more units of fertilizers are applied.

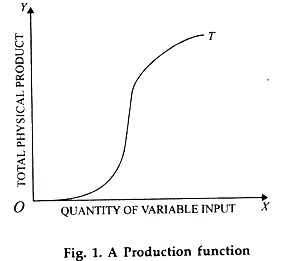
(b) The production function can also be illustrated geometrically by means of a simple graph as shown in Fig. 1. Input level is measured along the horizontal axis and the total output upon he vertical axis.

The points on the curve OT indicate different quantities of output associated with particular levels of the input used.

(c) The production function may be shown through an algebraic expression in which output is a dependent variable and input, the independent variable.

In algebraic form, it can be expressed as:

Y =f(x),

where Y represents the output, x, the input and ‘f’ means is a function of, or ‘depends upon, or is determined by’. Here, it is assumed that output depends upon a single factor. However, it must be understood that in actual life, agricultural output (and for that matter, any output) is never a function of a single factor. It rather depends upon a variety of factors, such as seeds, amount of fertilizers used, irrigation, nature of soil and so on. This can be written as:

Y = f (x₁, x₂, x₃………………….. x_n) + u

This function means that output depends upon all factors represented by x₁, x₂ etc., and also the level of unknown or uncontrollable factors represented by u. It is not feasible to consider all controllable factors simultaneously in any one study.

Therefore, each factor may be studied in combination with some factors considered as fixed. For illustration, a farmers may be interested in knowing how the output of wheat will change as the two inputs namely, the seeds and fertilizers are changed while other factors are held constant at fixed levels.

Types of Production Function:

We should note that a production function expresses a unique relationship between total output and the various inputs. Generally, the total output increases with an increase in inputs. Like any other function, all such functions where total output increase as the inputs increase, are known as increasing production functions,

There are also situations in the real world where an increase in inputs, instead of bringing about an increase in the total output, may decrease it. Such a production function will be known as decreasing production function.

It is necessary to explain these two types of functions in some detail:

(A) Increasing Production Function:

Though, in case of such functions, the mathematicians do not generally discuss the way the production increases when the inputs increase, an economist has to give considerable attention to this aspect.

From his point of view, it is important to know whether the rate of increase in production in response to successive equi-proportional changes in all inputs taken together (expressed in terms of returns to scale) or to successive changes in the amount of single input taken in isolation (expressed in terms of returns to a variable factor), is itself increasing, is constant or is decreasing. In other words, he is deeply interested in knowing whether the marginal returns to scale or the marginal returns to a variable factor are increasing, constant or decreasing.

We may note here that in case of productions planning, it is the marginal returns to a variable factor which are the main focus of attention. As such, in the paragraphs that follow, we shall be explaining the increasing production function by categorizing it into parts, on the basis of constant, increasing, and decreasing marginal returns to a variable input (For this purpose, we consider change in production in response to change in one input only. We assume other variable inputs to be constant. Such an approach simplifies the analysis. At a later stage, we shall see that analysis pertaining to one input can be easily extended to over other inputs also).

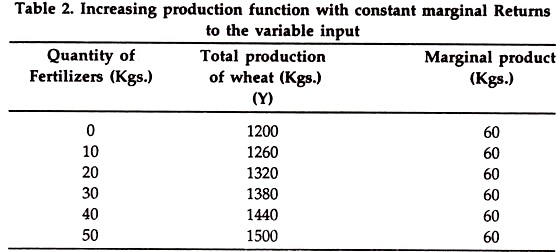
(i) Increasing production function with constant marginal returns to the variable input. In this function, the total production increases by the same magnitude for each additional unit of input used. For example, consider the following hypothetical relationship between fertilizers used and the total yield of wheat.

 

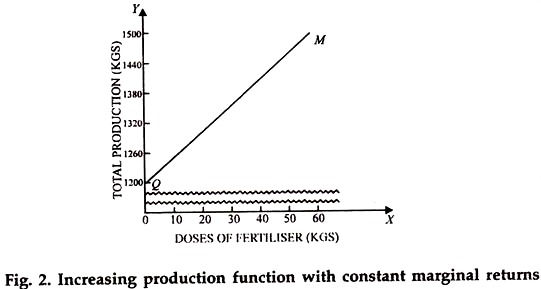
Graphic representation of this function will be a linear increasing function as shown in Fig. 2.

The diagram shows that each successive dose of 10 Kg. fertilizers makes a contribution of 60 kgs. Of wheat to the total output. We rarely come across this type of relationship in agriculture.

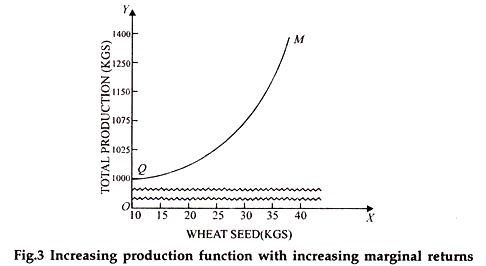
(ii) Increasing production function with increasing marginal returns on the variable input:

In this case, every successive dose of input brings about an increasing addition to the total output i.e., the output increasing rate when more and more units of an input are used. This type of relationship generally emerges when the fixed factors being used in production are having an excess capacity and use of additional units of the variable input results in a better utilisation of these fixed factors. The following table shows this type of production function.

Graphically this functional relation appears in the form of a curve. The curve becomes steeper as the input increases. Fig. 3 shows the increasing production with increasing marginal returns to the variable input. The curve that emerges in case of such a production function is concave downwards to X-axis as shown in the following diagram.

This type of relationship has been observed in agriculture but only over fairly short ranges of production.

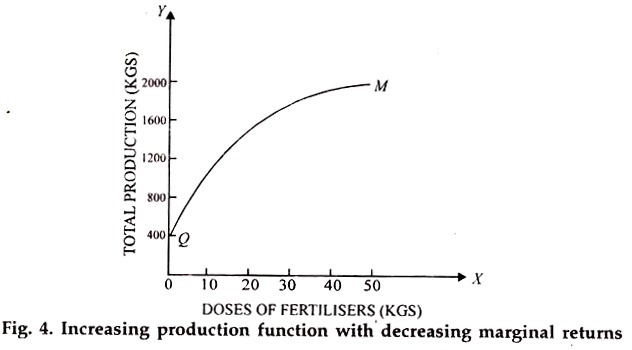
(iii) Increasing production function with decreasing marginal returns to the variable factor:

In this case, we find that though the total production increases as the input increases, each successive increase in output brought about by an additional dose of input declines. In other words, marginal returns to the input, though positive are declining. The following schedule shows his type of increasing production function.

Diagrammatically, the curve representing this type of production function will be concave upwards with regard to X-axis. Fig. 4 shows this curve.

We find that as each successive increase in output due to the use of an additional dose of input is declining, the curve becomes flatter as it moves towards the right.

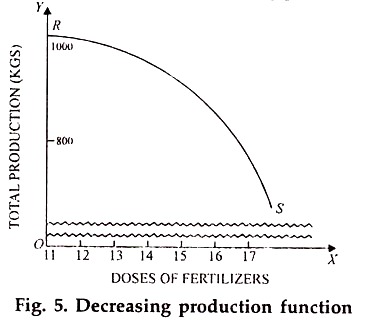
(B) Decreasing Production Function:

A decreasing production function is one in which the total output declines when the input increase. In terms of marginal returns to the variable factor, one could say that it is negative (less than zero).

The decreasing production function could also be divided into three categories on the basis of increasing, decreasing or constant rate of decrease in output. However, as we shall see later, no rational producer will ever operate in a situation (or stage) of decreasing production function i.e., where the total production declines as the input is increased.

As such, the exercise concerning categorization of the decreasing production function on the basis of the nature of its (negative) marginal returns to the variable input will have no practical utility.

The table 5 shows the decreasing production function: In this Table we have started with the 11th dose of fertilizers and not with the first dose. This is because it will be rather unrealistic to assume, that after the very first dose of fertilizers, the output starts decreasing.

The following diagram shows the decreasing production function:

The decreasing production function implies a line or a curve with negative slope. The curve can be concave or convex to the origin depending upon whether the output declines at an increasing rate or at a decreasing rate when more and more doses of an input are used.