Study Notes on Prisoner’s Dilemma | Oligopoly Models

The following points will highlight the top two things to know about prisoner’s dilemma. The things are: 1. Competition versus Collusion — Prisoners’ Dilemma 2. Implication of the Prisoners’ Dilemma: For Oligopolistic Pricing.

Prisoner’s Dilemma # 1. Competition versus Collusion — Prisoners’ Dilemma:

A Nash Equilibrium is a non-cooperative equilibrium, each firm decides that which gives it the highest possible profit, given the action of its competitors.

As we know, the resulting profit is higher than it would be under perfect competition, but lower than if the firms colluded.

Collusion may not be legal in many countries. But if cooperation can lead to higher profits, why do not firms cooperate without colluding? In practice, it may be possible to find out the profit-maximising price and to charge that price (without colluding) which is illegal and both can earn more profit.

The problem is that the competitor might not choose to set price at a collusive level Why not? Because your competitor would do better by choosing a lower price, even if it knows that you are going to charge price at the collusive level.

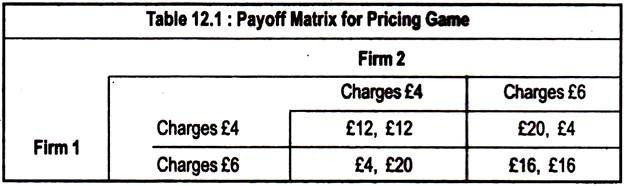
This would be clear if we go back to our price competition model where the firms have a fixed cost of £20, and have zero variable cost, and face the following demand curves:

Firm 1’s demand curve: Q₁ = 12 – 2P₁ + P₂……………….. (6)

Firm 2’s demand curve: Q₂ = 12 – 2P₂ + P₁………………. (7)

We found that, in the Nash Equilibrium, each firm will charge a price of £4 and earn a profit of £12, whereas, if they collude, price will be £6 and they earn a profit of £16 each.

Now, suppose, the firms do not collude, but Firm 1 sets a collusive price, hoping that Finn 2 will do the same.

If Firm 2 does the same, it will earn a profit of £16.

But what will happen if it charges the price of £4, instead?

Then, Firm 2 would be able to earn a higher profit of π₂ = P₂Q₂ – 20 = [12 – (2) (4) + 61 (4) -20 = £20

On the other hand, Firm 1 will earn a profit of:

π ₁ = P₁Q₁ -20 = (6) [12 – (2) (6) + 4] – 20 = £4

This exercise shows that if Firm 1 charges collusive price of £6, whereas, Firm 2 charges a price of £4, it will increase its profit to £20 and it will do so at the expense of Firm l’s profit, which will fall to £4. It is clear that Firm 1 can also do the same and earn higher profits at the expense of Firm 2. Each Firm does best by charging £4 and, thus, undercutting the other.

These different pricing possibilities are summarised in Table 12.1. In deciding what price to set, the two firms are playing a non-cooperative game — each firm does the best it can, independently, taking its competitor into account.

Table 1 is called the payoff matrix for this game as it shows the profit to each firm on the basis of its decision and the decision of its competitor. For example, the payoff matrix tells us that if both firms charge £4, each firm will make a profit of £12. It also tells us that if Firm 1 charges £4 and Firm 2 charges £6, Firm 1 will make £20, and Firm 2 will make £4 and so on:

The payoff matrix can give the answer to our original question; why do not firms behave cooperatively to earn higher profits, even if they cannot collude?

Cooperation means both firms charge £6 instead of £4, so that they can earn £16 profit rather than £12. The main reason is that each firm always makes more money by charging £4, no matter what its competitor does.

As the payoff matrix shows, if Firm 2 charges £4, Firm 1 does best by charging £4. And, if Firm 2 charges £6, Firm 1 still does best by charging £4. Similarly, Firm 2 always does best by charging £4, no matter what Firm 1 does. Unless the firms can sign an enforceable agreement to charge £6, neither firm can expect its competitor to charge £6, and both will charge £4.

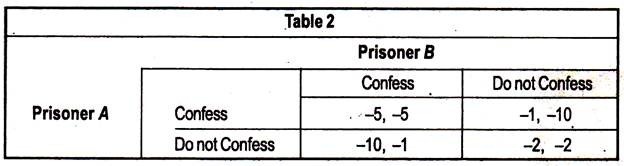
A classical example in game theory, called the Prisoners’ Dilemma, explains the problem oligopolists face. It can be explained as follows: Two prisoners have been accused of collaborating in a crime. They were kept in separate cells and each has been asked of their guilt.

If they both confess, each will receive a prison term of five years. If neither confesses, they both receive a term of two years. On the other hand, if one confesses and the other does not, the one who does will receive a term of only one year, while the other will receive a prison term of ten years. If you were one of these prisoners, what would you do — confess or not confess?

The payoff matrix in Table 12.2 summarizes these possibilities. It shows the prisoners’ dilemma. If they could both agree not to confess, each would go to jail for two years only. But they cannot talk to each other, and even if they could, can they trust each other? If prisoner A does not confess, he risks being taken advantage of by prisoner B.

No matter what prisoner A does, prisoner B will benefit by confessing. Similarly, prisoner A will always be ahead by confessing; so prisoner B must worry that, by not confessing, he will be taken advantage of. Thus, both of them will probably confess and go to jail for five years!

Oligopolist firms often find themselves in prisoners’ dilemma, in that they must decide whether to compete aggressively and capture a large share of the market at the expense of their competitors or to “cooperate” and coexist with the competitor with the market share they currently hold, and, perhaps, implicitly collude.

If the firms compete passively, setting high prices and limiting output, they will make higher profits than if they compete aggressively.

However, like prisoners, each firm has an incentive to undercut its competitors, and also its competitors have the same incentive. It is desirable to cooperate with the competitors, instead of competing aggressively, but the problem is its competitor might compete aggressively and take the lion’s share of the market.

As we have seen, in the pricing problem given in Table 12.1, both firms do better by “cooperating” and charging a high price. But the firms are in prisoners’ dilemma, where neither firm can trust or expect its competitor to set a higher price.

Prisoner’s Dilemma # 2. Implication of the Prisoners’ Dilemma: For Oligopolistic Pricing:

Does the prisoners’ dilemma force oligopolistic firms to aggressive competition and low profit? It may not be necessary, like our prisoners, to have only one opportunity to confess. Most firms set price and output over and over again, continually observing their competitors’ behaviour and adjusting their own accordingly.

This allows firms to develop a reputation from which trust can arise. As a consequence, oligopolistic coordination and cooperation may prevail.

For example, suppose an industry is made up of two or three firms which have coexisted for a long time.

Over the years, the managers of those firms might have become tired of losing money because of wars, and an implicit understanding might have developed in which all the firms charge high prices, and no firm makes a serious effort to take market share from its competitors which they know will be short-lived and the result will be renewed warfare and lower profits over the long-run.

The resolution of the prisoners’ dilemma may be possible in some industries, but not in others. Sometimes managers are not content with the moderately high profits resulting from implicit collusion but prefer to compete aggressively and wish to capture most of the market. Sometimes implicit understandings are difficult to reach and even harder to maintain.

As a result, in many industries, implicit agreement is short-lived. There is, often, a fundamental mistrust and, so, ‘war of the business-world’ may erupt out of a simple pretext.