Stackelberg’s Duopoly Model (With Diagram)

This model was developed by the German economist Heinrich von Stackelberg and is an extension of Cournot’s model.

It is assumed, by von Stackelberg, that one duopolist is sufficiently sophisticated to recognise that his competitor acts on the Cournot assumption.

This recognition allows the sophisticated duopolist to determine the reaction curve of his rival and incorporate it in his own profit function, which he then proceeds to maximise like a monopolist.

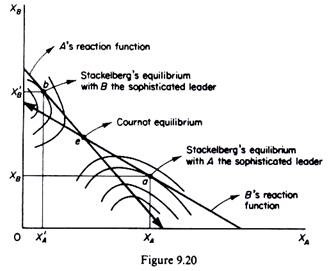
Assume that the isoprofit curves and the reaction functions of the duopolists are those depicted in figure 9.20. If firm A is the sophisticated oligopolist, it will assume that its rival will act on the basis of its own reaction curve. This recognition will permit firm A to choose to set its own output at the level which maximizes its own profit. This is point a (in figure 9.20) which lies on the lowest possible isoprofit curve of A, denoting the maximum profit A can achieve given B’s reaction curve.

Firm A, acting as a monopolist (by incorporating B’s reaction curve in his profit-maximizing computations) will produce X_A, and firm B will react by producing X_B according to its reaction curve. The sophisticated oligopolist becomes in effect the leader, while the naive rival who acts on the Cournot assumption becomes the follower.

Clearly sophistication is reward­ing for A because he reaches an isoprofit curve closer to his axis than if he behaved with the same naivete as his rival. The naive follower is worse off as compared with the Cournot equilibrium, since with this level of output he reaches an isoprofit curve further away from his axis.

If firm B is the sophisticated oligopolist, it will choose to produce X’_B, corresponding to point b on X’s reaction curve, because this is the largest profit that B can achieve given his isoprofit map and A’s reaction curve. Firm B will now be the leader while firm A becomes the follower. B has a higher profit and the naive firm A has a lower profit as compared with the Cournot equilibrium.

In summary, if only one firm is sophisticated, it will emerge as the leader, and a stable equilibrium will emerge, since the naive firm will act as a follower.

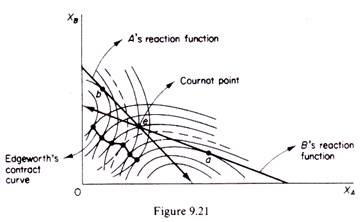
However, if both firms are sophisticated, then both will want to act as leaders, because this action yields a greater profit to them. In this case the market situation becomes unstable. The situation is known as Stackelberg’s disequilibrium and the effect will either be a price war until one of the firms surrenders and agrees to act as follower, or a collusion is reached, with both firms abandoning their naive reaction functions and moving to a point closer to (or on) the Edge-worth contract curve with both of them attaining higher profits. If the final equilibrium lies on the Edge-worth contract curve the industry profits (joint profits) are maximised (figure 9.21).

Von Stackelberg’s model has interesting implications.

It shows clearly that naive behaviour does not pay. The rivals should recognise their interdependence. By recognizing the other’s reactions each duopolist can reach a higher level of profit for himself. If both firms start recognising their mutual interdependence, each starts worrying about the rival’s profits and the rival’s reactions. If each ignores the other, a price war will be inevitable, as a result of which both will be worse off.

The model shows that a bargaining procedure and a collusive agreement becomes advantageous to both duopolists. With such a collusive agreement the duopolists may reach a point on the Edge-worth contract curve, thus attaining joint profit maxi­misation.

It should be noted that Stackelberg’s model of sophisticated behaviour is not appli­cable in a market in which the firms behave on Bertrand’s assumption. In a Cournot-type market the sophisticated firm ‘bluffs’ the rival, by producing a level of output larger than the one that would be produced in the Cournot equilibrium and the naive rival, sticking to his Cournot behavioural reaction pattern, will be misled and produce less than in the Cournot equilibrium.

However, in a Bertrand-type market the sophisticated duopolist can do nothing which would increase his own profit and persuade the other to stop price-cutting. The most he can do is to keep his own price constant, that is, behave exactly as his opponent expects him to behave.

If both entrepreneurs adopt Stackelberg’s sophisticated pattern of behaviour, each will examine his profits if he acts as a leader and if he acts as a follower, and will adopt the action that will yield him the greatest profit.

Firm A calculates its profits both as a leader and as a follower:

If A is the leader his profits are 3267

If A is the follower his profits are 3003

Clearly firm A will prefer to act as the leader.

Firm B similarly, calculates its profits as a leader and as a follower:

If B is the leader his profits are 918-75

If B acts as the follower his profits are 155-50

Thus firm B will also choose to act as the leader.

With both firms acting in the sophisticated way implied by Stackelberg’s behavioural hypothesis both will want to act as leaders. As they attempt to do so they find that their expecta­tions about the rival are not fulfilled and ‘warfare’ will start, unless they decide to come to a collusive agreement.

We may now summarise Stackelberg’s model. Each duopolist estimates the maximum profit that he would earn (a) if he acted as leader, (b) if he acted as follower, and chooses the behaviour which yields the largest maximum.

Four situations may arise:

(1) Duo­polist A wants to be leader and B wants to be follower.

(2) Duopolist B wants to be leader and A wants to be follower.

(3) Both firms want to be followers.

(4) Both firms desire to be leaders.

In situations (1) and (2) the result is a determinate equilibrium (provided that the first- and second-order conditions for maxima are fulfilled).

If both firms desire to be followers, their expectations do not materialize (since each assumes that the rival will act as a leader), and they must revise them. Two behavioural patterns are possible. If each duopolist recognises that his rival wants also to be a follow­er, the Cournot equilibrium is reached. Otherwise, one of the rivals must alter his be­haviour and act as a leader before equilibrium is attained.

Finally, if both duopolists want to be leaders a disequilibrium arises, whose outcome, according to Stackelberg, is economic warfare. Equilibrium will be reached either by collusion, or after the ‘weaker’ firm is eliminated or succumbs to the leadership of the other.