Chamberlin’s contribution to the theory of oligopoly consists in his suggestion that a stable equilibrium can be reached with the monopoly price being charged by all firms, if firms recognize their interdependence and act so as to maximize the industry profit (monopoly profit).
Chamberlin accepts that if firms do not recognize their interdependence, the industry will reach either the Cournot equilibrium.
If each firm acts independently on the assumption that the rivals will keep their output constant; or the industry will reach the Bertrand equilibrium if each firm acts independently, trying to maximize its own profit on the assumption that the other rivals will keep their price unchanged.
Chamberlin, however, rejects the assumption of independent action by competitors. He says that the firms do in fact recognize their interdependence. Firms are not as naive as Cournot and Bertrand assume. Firms, when changing their price or output, recognize the direct and indirect effects of their decisions. The direct effects are those which would occur if competitors were assumed to remain passive (either in the Cournot or in the Bertrand sense).
ADVERTISEMENTS:
The indirect effects are those which result from the fact that rivals do not in fact remain passive but react to the decisions of the firm which changes its price or output. The recognition of the full effects (direct and indirect) of a change in the firm’s output (or price) results in a stable industry equilibrium with the monopoly price and monopoly output.
Chamberlin assumes that the monopoly solution (with industry or joint profits being maximized) can be achieved without collusion the entrepreneurs are assumed to be intelligent enough to quickly recognize their interdependence, learn from their past mistakes and adopt the best (for all) position, which is charging the monopoly price.
Chamberlin’s model can best be understood if presented in a duopoly market. Initially Chamberlin’s model is the same as Cournot’s. The market demand is a straight line with negative slope, and production is assumed costless for simplicity (figure 9.15). If firm A is the first to start production it will produce the profit-maximizing output 0X M and sell it at the monopoly price PM.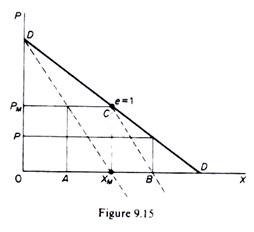 
Firm B, under the Cournot assumption that the rival A will retain his quantity unchanged, considers that its demand curve is CD and will attempt to maximize its profit by producing one-half of this demand, that is, quantity XMB (at which B’s MR = MC = 0). As a consequence the total industry output is OB and the price falls to P. Now firm A realizes that its rival does in fact react to its actions, and taking that into account decides to reduce its output to 0A which is one-half of 0XM and equal to B’s output.
The industry output is thus 0XM and price rises to the monopoly level 0PM. Firm B realizes that this is the best for both of them and so will keep its output the same at XMB = AXM. Thus, by recognizing their interdependence the firms reach the monopoly solution. Under the assumption of our example of equal costs (that is, costs = 0) the market will be shared equally between A and B (clearly 0A = AXM).
ADVERTISEMENTS:
Chamberlin’s model is an advance over the previous models in that it assumes that the firms are sophisticated enough to realise their interdependence, and that it leads to a stable equilibrium, which is the monopoly solution.
However, joint profit maximisation via non-collusive action implies that firms have a good knowledge of the market-demand curve and that they soon realise their mistakes. That is, they somehow acquire a knowledge of the total-supply curve (i.e. of the individual costs of the rivals) and hence they define the (monopoly) price which is best for the group as a whole. Without collusion joint profit maximisation is impossible unless all firms have identical costs and demands.
Chamberlin’s small group model suffers also from the defect of ignoring entry. It is a ‘closed’ model. If entry does occur it is not certain that the stable monopoly solution will ever be reached, unless special assumptions are made concerning the behaviour of the old firms and the new entrant.
It should be noted that although the ‘kinked-demand curve’ appears in Chamberlin’s analysis (of both the ‘large group’ and the ‘small group’), he does not use it explicitly as a tool of analysis of the behaviour of the firm. The ‘kinked-demand curve model’ as an operational oligopoly model was presented by P. Sweezy in 1939. We turn to the examination of this model.