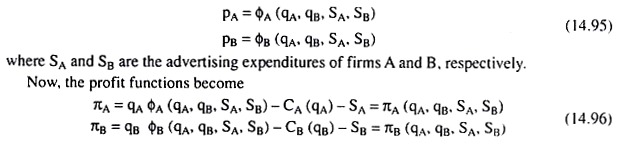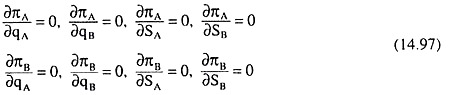Differentiated Products of Duopoly and Oligopoly | Product Markets

The differentiated oligopoly and duopoly, that is, where there is product differentiation as in the case of monopolistic competition. The individual producer of a differentiated product under oligopoly faces his own dis­tinct demand function.

The quantity demanded of his product would depend upon the pric­ing decisions of all the firms in the industry, and we may write the ith seller’s demand function as

q_i = f_i (p₁, p₂…….. p_n), i = 1, 2, .. ., n                                         (14.88)

In (14.88), an increase in price of the ith seller, with all other prices remaining unchanged, results in a reduction of his output level, i.e., here we have ∂q_i/∂p_i < 0. This is because, as the ith seller increases the price of his product with all other prices remaining unchanged, some of his customers will switch over to the products of the other sellers.

Again, if any of his rivals in­creases his price, then the ith seller can sell a larger quantity at the same price, i.e., in (14.88) we would also have > 0 for all ∂q_i/∂p_i. Because, now some customers of the rival’s product would turn to his product.

Difference with Monopolistic Competition:

There is product differentiation under monopolistic competition also. But there is an important difference. Under monopolistic competition, the number of sellers is large. So if there is a price change on the part of any one seller, then the effect of this upon the other sellers would be imperceptibly small.

Therefore, the sellers here behave as if they are independent of each other. But the number of sellers under oligopoly is very small. That is why the effect of a price change on the part of any one seller upon the other sellers is not imperceptible.

So the sellers here react to changes, if there be any, in the price of the product of a rival pro­ducer. In other words, the sellers in an oligopolistic or a duopolistic market are not independ­ent, they are interdependent.

Profit Maximisation by an Individual Seller under Differentiated Oligopoly:

Individual producers can set either price or quantity to be sold or demanded. They cannot dictate both. The inverse of the demand function (14.88) of an individual seller (the ith seller) may be written as

p_i = F_i (q₁, q2…………. q_n),i =1, 2,…,n                                    (14.89)

All partial derivatives of p_i in (14.89) are negative. For, if the ith seller increases his quantity sold (q_i), with all other output levels constant, will fall, since a larger quantity can be sold only at a lower price. That is, we would have ∂q_i/∂p_i < 0.

Also, if some other seller increases his output level (q_j, j ≠ i), his price (p_j) will decline, (i.e., ∂q_i/∂p_i < 0) and the ith seller will also have to decline p_i if q_i is to be maintained at a constant level.

Otherwise the product of the ith seller will become relatively dearer and some of his customers would switch over to the prod­ucts of his rivals (i.e., ∂q_i/∂p_i < 0). Let us now see how the duopoly firms under product differentiation may pursue the goal of profit maximisation.

In order to do this, we have to replace the market demand function of undifferentiated duopoly:

If we now solve the equations (14.94), we would obtain the profit-maximising prices and outputs of the duopolists, provided the second order conditions are satisfied. Under product differentiation, the profits of the duopolists may also depend upon the amounts of their advertising expenditures.

For advertising may allow a firm to sell a larger quantity at a given price, or, a given quantity at a higher price. Therefore, under advertising, the inverse demand functions of the two firms would be

Since π_A and π_B are functions of q_A, q_B, S_A and S_B, they would have to be maximised w.r.t. these independent variables. The FOCs for profit maximisation of the duopolists would be given by

If the above equations (14.97) are solved, we would obtain the profit maximising values of q_A, q_B, S_A, S_B and the maximum values of π_A and π_B, provided the second order conditions are satisfied. We have seen in the above analysis how an individual seller under differentiated oligopoly may proceed to achieve his goal of profit maximisation.

Let us note here that we may easily introduce product differentiation in the Cournot, Stackelberg and collusive oligopoly models if we replace the market demand function