Let us make an in-depth study of the Convergence Hypothesis. After reading this article you will learn about: 1. Types of Convergence 2. Possible Paths of Convergence.
Types of Convergence:
There are three types of convergence unconditional convergence, conditional convergence and no convergence.
(i) Unconditional Convergence:
By unconditional convergence we mean that LDCs will ultimately catch up with the industrially advanced countries so that, in the long run, the standards of living throughout the world become more or less the same. The Solow model predicts unconditional convergence under certain special conditions. For example, let us suppose that different countries of the world differed mainly in their capital-labour ratios.
ADVERTISEMENTS:
Normally, rich countries have high capital-labour ratio and high levels of output per worker. By contrast, low income countries have low capital-labour ratios and low levels of output per worker. We also assume that two groups of countries are the same in all other respects such as saving rates, population growth rates and the production function.
If this is true then the Solow model predicts that, in spite of any differences in initial capital-labour ratios, all these countries will ultimately attain the same steady state. Differently put, if countries have the same fundamental characteristics, capital-labour ratios and living standards will unconditionally converge, even though some countries may start from way behind.
(ii) Conditional convergence:
Even if countries differ in their saving rates, population growth rates and production functions (due to unequal access to technology) they will converge to different steady state with different capital-labour ratios and different standards of living in the long run. If countries differ in the fundamental characteristics, the Solow model predicts conditional convergence.
ADVERTISEMENTS:
This means that standards of living will converge only within groups of countries having similar characteristics. For example, if there is conditional convergence, a low income country with a low saving rate may catch up, one day or the other, a richer country that also has a low saving rate, but it will never catch up a rich country that has a high saving rate.
One reason for this is that poor countries have less capital per worker and thus higher marginal products of capital than do rich countries. So savers in all countries will be able to earn the highest return by investing in poor countries. Eventually, borrowing abroad will allow initially poor countries’ capital-labour ratios and output per worker to be the same as in initially rich countries.
(iii) No convergence:
The third possibility is no convergence. This means that the low income countries will never catch up over time. Therefore living standards may even diverge due to widening income gap — the rich getting richer and poor getting poorer.
Possible Paths of Convergence:
ADVERTISEMENTS:
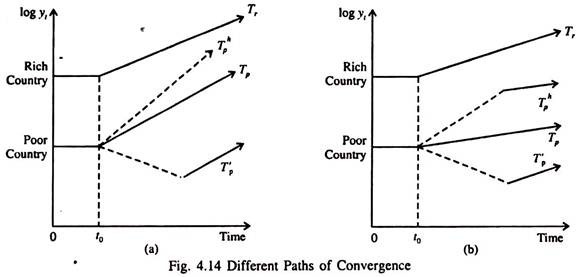
In Fig. 4.14(a) and 4.14(b) we show the possible paths of convergence and divergence of per capita output. In Fig. 4.14(a) Tr represents the steady state growth path of the rich country. The slope of this line represents the rate of growth for the poor country. Three options are open to them.
Here Tp represents a steady state growth path in which the rich and poor countries grow at the same rate. A favourable shock at time t0 leads to convergence of output per capita in rich and poor countries as shown by the steady state growth path Tp.
An adverse shock that slows down the growth rate of the poor country in the short run but leads to the same steady state growth as in Tp is indicated by the growth path T’p. The dotted line indicates movement outside of steady state.
Fig 4.14(b) shows divergence between the rich and poor countries. Tr and T represent the steady state growth paths of the rich and poor country. We find divergence of per capita outputs across two countries over time. Here the scenario is different.
Irrespective of favourable shock (Th) or an adverse shock (T’p) the steady state growth rate is the same as in Tp, and long-run income per capita in the rich country will increasingly diverge from that in the poor country. The solid lines in both diagrams are steady state paths whereas the dotted lines represent transitions to equilibrium in response to a shock.
The path Th in Fig 4.14(a) shows how absolute convergence — in the sense of the same growth rates as also the same growth path — occurs. This is a strong form of convergence. A weaker form of convergence — called conditional convergence — is depicted by the paths T’p and Tp which show the same growth rates but different growth paths among countries.
The vertical distance of the growth path of a poor country from that of a rich country represents income differences due to differences in underlying parameters such as savings rates and population growth.
The developing countries can have free access to the technology developed by the pioneers. This implies that latecomers have a potential advantage over pioneers — an advantage of backwardness.
ADVERTISEMENTS:
In the course of adopting and adapting new techniques, IRS appear in the guise of learning-by-doing. No doubt the firms which adopt new techniques find an improvement in efficiency following the adoption.
Hence, if firms in LDCs organise themselves so as to profit from the accumulated experienced as fully as do firms in developed countries and such improvements have a ceiling that is reached in finite time or cumulative output, as seems plausible, then catching up in that particular time of production with the technique in question will be complete.
Unfortunately from the point of view of the world’s low income countries there is hardly any empirical support for unconditional convergence. Most studies have found little tendency for low income countries to catch up with their rich counterparts.