Technological Progress and Economic Growth | Economics

Technological change is the most important factor that determine rate of economic growth. It plays a important role than the capital formation. It is the technological change which can bring about continued increase in output per head of the population. Thus it is the prime-mover of economic growth.

Technological change or progress refers to the discovery of the new and improved methods of producing goods. Sometimes technological advances result in the increase in available supplies of natural resources. But more generally technological changes result in increasing the productivity of labour, capital and other resources. The productivity of combined inputs of all factors is called total factor productivity. Thus technological progress means increase in total factor productivity. As a result of technological advance, it becomes possible to produce more output with same resources or the same amount of product with less resource.

But the question arises as to how the technological progress takes place. The technological progress takes place through inventions and innovations. The word invention is used for the new scientific discoveries, whereas the innovations are said to take place only when the new scientific discoveries are commercially used for actual production of goods. Some inventions may not be economically profitable to be used for actual production.

It follows from above that technological change brings about an increase in output per head. Thus technological change, or more precisely technological progress, is the change in the production process which results in an increased output per unit of labour. Technological change causes a shift in the production function embodying all known techniques. Technological change must be distinguished from a change in technique. While by technological change we mean advance in knowledge resulting in improved methods of production, change in technique refers to the use of a different but already known method of production.

The process of economic growth involves the increase in the production of goods and services. Increase in production can be achieved either through the use of more resources and/or through the realization of higher productivity by means of using the resources of labour, capital and land more efficiently. Technological change helps to promote growth in both these ways. It can help in the discovery of new natural resources in the country and thereby enhances the productive potential of the country. Technological change also increases the productivity of available resources.

For instance, it can find out the productive uses of land that hitherto has been regarded as infertile or it can discover new economic use of a raw material that had previously been considered as useless. But, as explained above, technological change more generally results in higher productivity of resources. Technological change raises the productivity of worker through the provision of better machines, better methods and superior skills.

Table 8.1 gives the percentage increase in labour productivity in a number of countries during the period 1970-1989. By bringing about increase in productivity of resources the progress in technology makes it possible to produce more output with the same resources or the same amount of output with less resource. Progress in technology causes improvement in technology through the provision of better machines, better methods and enhanced skills.

It is technology which underlies the process of producing new things with the existing resources or using the existing resources in new ways. This is what Schumpeter means when he says that, “the slow and continuous increase in the national supply of productive means and savings is obviously an important factor in explaining the course of economic history through the centuries, but it is completely overshadowed by the fact that development consists primarily in employing existing resources in a different way, in doing new things with them, irrespective of whether those resources increase or not. It is important to emphasize that newly discovered techniques lead to the increase in output per worker.”

Productivity of workers depends upon the quantity and quality of capital tools with which they work. For higher productivity the instruments of production have to be technologically efficient and superior. The technological options open to an economy determine the input mix of production. A commodity can be produced by various technologies. The quantity and quality of capital, skills and other factors required for production is directly dependent on the efficiency of the technique of production being used. Also, the managerial and organisational expertise has to be in line with the technological requirements of production. Thus, technology in the present stage of economic development is an indispensable factor of production.

This is the age of technology. The developing countries are obsessed by the desire to make rapid progress in technology so as to catch up with the present-day developed countries. Frantic efforts are being made to install improved technology in agriculture, industries, health, sanitation and education; in fact in all walks of human life. Indeed, the newly emerging nations have come to regard technology as a bastion of national autonomy and as a status symbol in the international community.

It will be noticed that during 1970-89 rate of increase in labour productivity for the United States is less than other countries except Canada and Sweden. Slow growth in productivity in the Unites States during the period (1970-89) had been a major concern and was the subject of debate among the economists. It will be further observed that during this period Japan had the highest growth rate in labour productivity of 6% followed by Italy and Netherlands.

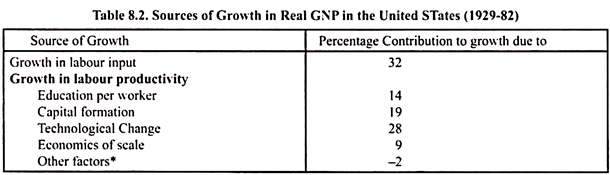
Denison in his empirical study has estimated the sources of increase in real GNP between 1929 and 1982 of the United States. He found that technological change contributed 28% to the average annual growth in real GNP which was 2.9 per cent over this period. The estimates of contribution of various factors such as labour, education and capital are presented in Table 8.2.

From the table it will be seen that increase in the quantity of labour contributed to 32 per cent to 2.9 per cent annual growth in the United States. The other Factors contribute to the annual growth by raising productivity of labour.

Technical progress manifests itself in the change in production function. So a simple measure of the technical progress would be the comparison of the position of production function at two points of time. The technological change operates upon the production function through improvements of various sorts such as superior equipment, an improved material, and superior organisational efficiency. Also, the technological progress may express itself in making available new products. The availability of a new product in many cases could be construed as a change in the production function as it can be regarded equivalent to a more efficient way of meeting an old want.

Technological Change and Capital Formation:

The process of technological progress is inseparably linked with the process of capital formation. In fact, both go hand in hand. Technological progress is virtually impossible without prior capital formation. It is because the introduction of superior or more efficient techniques requires the building up of new capital equipment which incorporates new technology. In other words, new and superior technology can contribute to national product and its growth if it is first embodied in the new capital equipment.

The capital accumulation has, therefore, been called the vehicle for the steady introduction of new technology into the economy –

It may be noted that Adam Smith viewed technological progress as a rise in productivity of workers as a result of increase in division of labour and specialization. This leads to the growth in national income. But it was J.A. Schumpeter who laid great stress on the role of technological innovations in bringing about economic growth. He visualised technical innovations in bringing about economic progress. It is the entrepreneur who carries out the innovations and organises the production structure more efficiently. As, according to Schumpter, the innovations occur in spurts rather than in a smooth flow, economic progress is not an uninterrupted process. The pace of economic progress is punctuated by the pace of innovations. Since innovations are governed by a host of factors, therefore, it is difficult to predict about the economic progress resulting from technological changes.

Prof. Rostow has proposed four stages in the development of an economy.

These stages are:

(i) Traditional society;

(ii) Preconditions for takeoff;

(iii) Drive to maturity and

(iv) Stages of high mass consumption.

It may be noted that the economic transformation of the society from one stage to another involves, along with other things, a change in the level and character of technology. In the present age of greater specialisation it is the technology factor that underlines all major aspects of the modern productive apparatus such as decision making, production programming, and skill requirements market strategy.

The role of technological progress in economic development has not only been large but also increasing over time. It is beyond any doubt that the inventions and changes in production techniques played more important role in the late eighteenth and later centuries than in the earlier ones. The technical innovations provided the motive force for the industrial revolution in Western Europe. While the innovations mainly arose because of input shortages, they tended to overcome the impediments to mass production and the transport bottlenecks in the movement of industrial raw materials and labour. There were also improvements in managerial organisation with a view to reduce costs of production. The adjustments in the product designs also took place to meet the variations in the wants of the people.

Technical progress is the prime mover of economic growth. A continuing technical progress ensures a continuing growth. Where there is no technical progress, capital accumulation alone may fail to bring growth beyond a point. For capital accumulation without technical progress can bring about growth in income per head only so long as the available labour force has not been fully equipped with the latest techniques available, and only so long as all the wants of the consumers have not been supplied to the full extent. Once that point is reached where all labour has been equipped with the latest techniques and all wants of consumers have been met to the full extent, growth would come to an end unless technical progress occurs.

Technological Progress to Overcome Stationary State:

It is now widely accepted that technological change raises productivity and that a continuous occurrence of technological change will enable the economy to escape from being driven to the stationary state or economic stagnation. Classical economists like David Ricardo and J.S. Mill expressed fear that the increase in the stock of capital will sooner or later land the economy into stationary state beyond which economic growth will come to an end. Classical economists remained occupied with the idea of a stationary state because they did not take into account technological progress that could postpone the occurrence of a stationary state and ensure continued economic growth. Indeed, if technological progress continuously takes place, demon of stationary state can be put off indefinitely.

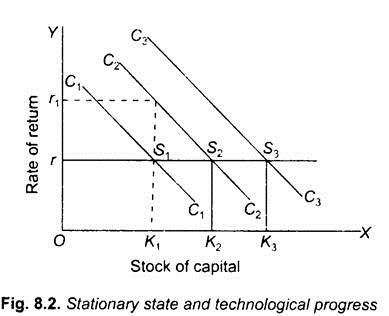
We can diagrammatically show how the technological change will raise productivity and thereby suspend the occurrence of stationary state with the help of Hicks’s representation of classical model. Let us first represent the classical model of stationary state. Let us consider Fig. 8.1 where along the X-axis stock of capital is measured and up the Y-axis rate of return on capital is measured. This rate of return on capital is in effect of the marginal productivity of capital. It may be noted that rate of return is here taken to be quite akin to the ‘ rate of interest’ which was regarded by the classical economists as the mechanism which determines investment to be made in any period of time.

Now, let us suppose that the economy has, at a particular moment, a stock of capital equal to K₁, in Fig. 8.1. Given this stock of capital, the rate of return which the businessmen would be able to earn from a new investment would be somewhat less than r₃ .However, if the economy is to be kept growing through capital accumulation while maintaining full employment, the rate of interest must be less than r₃; let us say it is at the level r₂. In this situation, it would be profitable for the businessmen, in the given period, say, one year, to undertake investment (through borrowing or with their own funds) to an extent that results in a net addition of K₁ K₂ to the capital stock. Therefore, at the end of the year, the economy would come to have K₂ amount of capital stock. It is possible now to draw a curve CC in Fig. 8.1 which indicates the different rates of return obtainable from the different levels of capital stock.

Assuming that the supply of labour is constant, in the absence of technological progress and consequently rate of return curve CC remaining the same, the expansion in the stock of capital from K₁ to K₂ will bring down the rate of return on capital from r₃ to r₂. As a result, the rate of return on new investment will now be slightly below r₂ after K₁K₂ investment has been undertaken in the year. Now, if there are still net positive savings in the community which is likely the case when capital stock has not yet sufficiently increased, then the rate of interest will fall below the level of r₂. With the fall in the rate of interest below r₂ and the rate of return on new investment being nearly equal to r₂ (i.e., only slightly less than r₂), it will be worthwhile to undertake new investment in the next year and in this way to maintain full employment in the next year.

According to the classical economists, rate of interest will continue falling gradually over time till it reaches a level at which both net saving and net investment have fallen to zero. In Fig. 8.1 this will take place when the capital stock has increased to K₃ and rate of interest has fallen to r₁. Since there are no more net savings and investment, the further expansion in the stock of capital and therefore the process of economic growth will cease to occur and the economy will reach what classical economists called stationary state. However, according to the classical economists, the stationary state is a distant end which may not be reached at all. This view of ‘classicals’, according to Hicks, is based on the idea that the curve CC is highly elastic, so that the distances such as K₁ K₂ are, indeed, very small. Thus, capital accumulation takes place by very small steps and can go on for a very long time before the rate of return finally falls to r₁.

Stationary State can be postponed through Technological Progress:

It may be noted that the businessmen would continue undertaking investments so long as the capital stock is less than K₃ .For, until K₃ level of capital stock is reached, the rate of return is high enough to induce businessmen to use the net savings for undertaking new investments. However, once the K₃ level of capital stock is reached, net savings would have fallen to the zero level and consequently both net investment and capital accumulation will cease to occur. While in this situation, net investment would necessarily have come to an end, gross investment may continue. But the gross investment does not add to capital stock; it is made just for the purposes of replacements of worn-out capital. When the stationary state has been reached, net investment would be zero because net savings are zero. Also, the population, income and standards of living would stabilise at a constant level.

Now, the importance of technological progress is that it can suspend the occurrence of stationary state equilibrium. Classical economists underestimated the role of technological progress in preventing the occurrence of stationary state equilibrium. When technical progress occurs it will raise the productivity of capital and labour. As a result of the rise in productivity, the rate of return curve CC (i.e., marginal productivity curve of capital) will shift upward.

This implies that it will be profitable to accumulate more capital and thereby suspending the occurrence of the stationary state. This is illustrated in Fig. 8.2 where to begin with economy is in stationary state equilibrium at point S₁ with rate of return on capital equal to r. Suppose that a new technological advance takes place which is embodied in a new machinery with which output per unit of labour is greater than before. As a result of this technological advance, the marginal productivity curve (i.e., curve of rate of return on capital) will shift upward.

As will be seen from Fig. 8.2, with the shift in the rate of return curve from C₁C₁ to C₂C₂ the rate of return on capital has risen to r₁. With the rate of return on new investment being nearly equal to r₁ and the rate of interest being equal to r, it will be profitable to undertake new investment. As a result, stock of capital will increase to the level K₂ and the whole of the given labour force has been equipped with new machines corresponding to the new technology.

With the increase in stock of capital to K₂, the rate of return will fall to r. Thus when the rate of return again falls to r level, the net saving and the net investment will be reduced to zero and a new stationary state equilibrium will be reached at S₂. With the stock of capital equal to K₂, suppose there occurs a new burst of technical progress which causes the CC curve to shift further upward to C₃C₃. This will cause the capital accumulation to take place further to K₃ .Thus a result of technological progress and more capital accumulation, output, income and the standards of living of the people will rise.

It follows from above that technological progress holds the key to economic growth. As technological progress takes place, capital accumulation will proceed further and economic growth will take place. Without technical progress, capital accumulation can raise the output and income to a limited extent. With constant labour force and the given technology, capital accumulation can lead to the increase in output so long as all the workers of the labour force are not equipped with the latest capital equipment embodying the latest technology. After this, technological progress can lead to the growth of output and income.

Thus, Professors Stonier and Hague rightly state – “Technical progress, therefore, turns out to be even more essential to economic growth than capital accumulation. Where there is no technical progress, capital accumulation can lead to growth in income per head only so long as labour force has not been fully equipped in accordance with the latest techniques. Once that happens, growth comes to an end. It is technical progress alone which ensures that the stationary state is not merely very far off but will never arrive so long as technical progress continues.”

Technological Change – Disembodied and Embodied:

The factors which cause sustained growth of national income and per capita income is an important issue that has been the concern of economists. Capital accumulation, growth in labour force and technological progress contribute to the growth of an economy. American economist R.M. Solow used the aggregate production function that relates the level of output to the levels of various inputs such as growth of capital, labour and technological progress over time. Solow used the following production function-

Y = A (t) F (K, L)…… (1)

Where, Y stands for output, K for capital and L for labour. The term A (t) represents technological change which is taken to depend merely on time, that is, as time passes, A (t) increases showing that over time technological progress enables more to be produced with the given quantities of capital and labour. With such specifications of production function, technological progress does not cause any change in the relative marginal productivities of capital and labour, that is, such technological progress brings about equal increases in the productivities of the two factors and is said to be Hicks’ neutral in the sense that it favours neither capital nor labour.

But the important thing to note in the production function given above is that it represents technological progress which is exogenous and disembodied. By exogenous technological progress we mean it comes from outside the model and, therefore, the term A (t) is shown outside the production function. Disembodied technological change raises the productivity of both old and new machines (i.e., capital goods) and does not depend on the rate of new investment.

The disembodied technological change is purely organisational in nature which permits more output to be produced from the given inputs without any new investment. That is, disembodied technological change causes a shift in the production function without disturbing capital-labour ratio. It is through organisational changes that disembodied technological change enables more output to be produced with existing inputs being used more effectively.

Disembodied technological change is represented in Fig. 8.3 where on the horizontal axis capital-labour ratio (K/L), that is, capital per worker is measured and along the vertical axis output per worker(Y/L) is measured .In the beginning, production function curve Y = f₁(k/L) is given and, according to this, with a capital per worker equal to K/L, level of output Y₁ is being produced.

Now, suppose that technological progress takes place and production function curve shifts upward to OY’ that is, to Y’ = f ₂(K/L). According to the new production function curve Y’ = f₂(K/L), with the given capital-labour ratio, K/L more output Y₂ is produced. Similarly, with any other capital-labour ratio on the new production function curve OY’, i.e., Y’ =f₂(K/L), more output will be produced as compared to that on the production function curve OY.

Embodied Technological Change:

In the embodied technological change, the increase in investment or capital accumulation is regarded as the vehicle of technological progress. Technological progress increases the productivity of new machines built in any period compared with old machines built in the previous periods. This implies that embodied technological change does not cause increase in the productivity of machine already in existence.

About embodied technological change, Hahn and Matthews in their review of the theory of economic growth write, “Technological change is embodied in new machines. Machines unalterably embody the technology of their date of construction. Machines built in different dates are therefore qualitatively dissimilar and cannot in the general case be aggregated into a single measure of capital. A separate production function is needed for each vintage. Total output is the sum of Output of all vintages in use”.

Production function of embodied technology can be written as –

Y_t =F (K_t, L_t, A_t,) … (2)

Where, output Y_t depends on the amount of capital (K_t), labour (L_t) and the level of technology (A_t). Note that in the production function (2), the term A_t for technology appears inside the production function as one of the endogenous inputs.

It is important to note that in the production function (2), the relationship between output and technology differs from the relationship between output and other inputs, capital and labour. This can be better understood by considering this production function in case of an individual firm which can be stated as –

Y_it= F (K_it, L_it, At) … (3)

The production function (3) of the individual firm shows that output of an individual firm depends not only on its own level of capital (K_it) and labour (L_it) but also on the economy-wide level of technology. Expressing production function in this way, the technological progress in the economy will increase the productivity of all firms including the firm whose production function (3) is given above.

In this formulation of production function, the technology is assumed to progress endogenously instead of being an exogenous change. Thus, in the concept of embodied technology, production function depends on the investment in new capital. Technological progress fosters inventions and improvements in machines. Thus new improved technology is embodied in investment in the new machines.

Neutral, Capital– Saving and Labour– Saving Technological Change:

It is important to know the difference between labour–saving and capital–saving technological change. But before explaining labour-saving and capital-saving technological change, it will be useful to make clear the meaning of neutral technological changes, since it is neutral technology which is the dividing line between labour-saving and capital-saving technological change. In economics neutral technological change (or innovation) has been defined in two ways, the first by J.R. Hicks and the second by R.F. Harrod.

These two concepts of neutral technological change are explained below:

Hicks’ Neutral Technological Change:

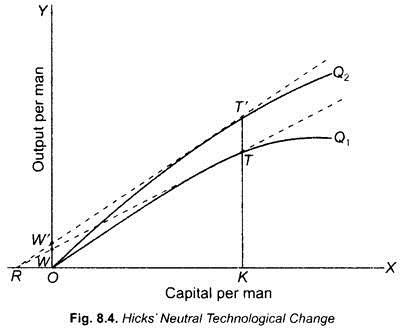
Hicks defined neutral technological change in the context of static price theory, especially in connection with the theory of wages. According to Hicks, neutral technological change (or neutral innovation) is one where if certain ratio of two factors, say, labour and capital, is being used to produce a given output, the effect of neutral technological change is to bring about increase in the marginal productivity of each factor in the same proportion. Hicksian concept of neutral technological change (neutral innovation) has been shown in Fig. 8.4 where along the X-axis, capital per man is measured and up the X-axis output per man is measured.

To the left of the origin O along the X-axis we represent the ratio of marginal products of labour and capital such as OR. The curve OQ₁ depicts the production function (total product curve) according to some existing technology. Suppose a technological change takes place and as a result production function shifts upward to OQ₂.

With production function OQ₁ and, before technological change in Fig. 8.4 the equilibrium is at point T on the production function OQ₁ where wage rate is equal to OW which is equal to the marginal product of labour. It should be noted that in Fig. 8.4 the slope of the curve TR represents the marginal product of capital as along the X-axis, capital per man is measured.

Now, the slope of the tangent, TR = TK/RK = OW/OR

It follows therefore that the marginal product of capital = OW/OR

If ν stands for marginal product of capital, then

ν = OW/OR

Manipulating the above equation we have –

OR = OW/ ν

As stated above, OW represents marginal product of labour and ν the marginal product of capital–

Therefore,

OR = Marginal Product of labour /Marginal Product of capital

It is, therefore evident that the distance OR measures the ratio between the marginal product of labour and the marginal product of capital in the position of equilibrium.

Now, if technological progress is to be Hicks-neutral, then technological change causing shift in production function from OQ₁ to OQ₂ should leave the ratio between the marginal product of labour and marginal product of capital unchanged at any given value of the capital-labour ratio. Since at the equilibrium position T in Fig. 8.4 the capital-labour ratio (i.e., capital per man) is OK, Hicks’ neutral technology requires that at the capital-labour ratio OK, the ratio of marginal product of capital to marginal product of labour remains the same (i.e., equal to OR) when technological change has taken place and production function has shifted to OQ₂.

This implies that when the new production function OQ₂ and at point ‘T’ corresponding to capital-labour ratio OK, if a tangent is drawn, it should pass through the same point R. It will be seen that such is the case in Fig. 8.4. With the slopes of the tangents RT’ and RT to production functions Q₂ and Q₁ being equal to OR implies that technological change brings about change in the marginal products of labour in the same proportion. It will also be observed from Fig. 8.4 that as a result of the technological progress and shift in production function, the output per man has increased and also the equilibrium wage rate has increased from OW to OW ‘. Thus both labour productivity and capital productivity has increased as a result of technological progress.

Capital-Saving and Labour-Saving Technological Change:

From Hicks’ definition of neutral technological change, the concepts of capital-saving and labour-saving technical change can easily be understood. A capital-saving technological change (capital-saving innovation) is that which, at a given capital-labour ratio, raises the marginal productivity of labour relative to the marginal productivity of capital. This means that it would now be possible to produce a given level of output with less capital relative to labour as a result of technological progress.

Thus technological change is capital-saving in the Hicksian sense when the ratio– Marginal Product of Labour/ Marginal Product of Capital or (ΔQ/ ΔL) / (ΔQ/ ΔK) increases, where ΔQ stands for a small change output in response to a small change in labour input (ΔL) and a small change in capital input (ΔK). Thus ΔQ/ΔL and ΔQ/ΔK will measure marginal product of labour and marginal product of capital respectively.

Note that capital-saving technological change generally implies labour-using technological change as labour is substituted for capital.

In terms of Fig. 8.4 if capital-saving technological change occurs, the production function will shift in such a way that the tangent drawn at point T ‘ (corresponding to the given capital-labour ratio OK) then that tangent will pass through the left of point R indicating that the ratio of marginal product of labour to marginal product of capital will increase. As a result, the given output can be produced with less capital relatively to labour. Therefore, it shows capital-saving innovation (i.e., technological change).

Labour-Saving Technological Change:

According to Hicks, labour-saving technological change is one which reduces the marginal product of labour relative to that of capital. In other words, labour- saving technological change (i.e., labour-saving innovation) occurs when at a given capital-labour ratio,

The ratio, Marginal product of Labour/ Marginal product of Capital or (MP_L/ MP_K) declines.

This implies that in case of labour-using technological change it would now be possible to produce a given level of output with less labour relative to capital following a change in technology. Note that labour-saving technological change generally implies capital-using technological change. In other words, in this case capital-intensity of production will increase. In terms of Fig. 8.4 the production function curve will shift in such a way that the tangent drawn at the new production function corresponding to the given capital-labour ratio OK will pass through the right of point R.

Harrod’s Neutral, Labour-Saving and Capital-Saving Technological Change:

It has been shown by R.F. Harrod, a prominent British economist, that Hicks’ concept of neutral change is heavily dependent on factors such as elasticity of demand for factors and products which are quite unrelated to the real character of technological change. Besides Hicks’ concept of neutral, technology has been developed in the framework of static economic theory. Therefore, an alternative concept of neutral technological change which is extensively used in the theory of economic growth has been put forward by R.F. Harrod in his now well-known work “Towards a Dynamic Economics”.

While Hicks’ concept of neutral technological change considers the ratio between the marginal products of the two factors when capital-labour ratio remains constant, Harrod states his concept of neutral technological change in terms of the relationship between rate of profit and capital-output ratio. According to Harrod, neutral technological change is that which leaves the capital-output ratio unchanged when rate of profit (assumed to be equal to marginal product of capital) remains constant. Thus when there is technological progress and rate of profit remains constant, technological change will be Harrod-neutral only if capital-output ratio also remains unchanged.

It follows from the definition of Harrod’s neutral technical change that when rate of profit remains constant after the technological change, technological progress would be labour-saving in the Harrodian sense if capital-output ratio rises. This means that now same output can be obtained by using more capital. Given the level of output, the use of more capital implies the substitution of capital for labour.

On the other hand, when there is technological progress and rate of profit remain the same, the technological progress would be capital-saving in the Harrodian sense if capital-output ratio falls. This implies that now the same output can be produced with less capital. Obviously, there is saving in capital as a result of substitution of labour for it. It is worthwhile to note that since in Harrod’s concept of neutral technological change, rate of profit and capital-output ratio remain constant, it means that distribution of income between profits and wages will remain unchanged following such a type of technological change. In terms of Harrod’s growth model, the implication of capital-output ratio remaining constant when a neutral technological change occurs is that relative shares of wages and profits in national income remains constant as balanced growth of national income takes place.

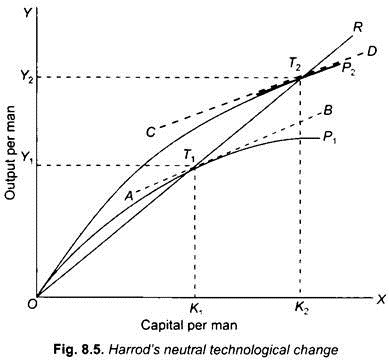
Harrod’s concept of neutral technological change is graphically illustrated in Fig. 8.5. In this figure, capital per man is measured along the X-axis and output per man is measured up the Y-axis. Initially, the production function curve is OP₁ showing the change in total output as capital per man increases. Suppose the economy is in equilibrium at point T₁ on the production function curve OP₁. At point T₁ on the production function curve OP₁, capital-output ratio is OK₁/OY₁.

The straight line OR passes through the origin. Therefore, all points on the straight line OR such as T₁ and T₂ represent the same capital-output ratio. Thus capital-output ratio at T₂ is equal to OK₂/OY₂.

Hence,

OK₂/OY₂=OK₁/OY₁

Suppose there is technical progress and as a result production function shifts from OP₁ to OP₂. The economy will now be in equilibrium at some point, say T₂, on the new production function OP₂. As the points T₁ and T₂ lie on the same straight line OR passing through the origin, capital-output ratio at the equilibrium position before and after the assumed technical change has remained unchanged.

But for technological change to be neutral in the Harrodian sense, not only capital-output ratio should remain the same but also rate of profit should remain unchanged as production function changes and we move along the ray OR representing a given level of capital-output ratio. Now, the rate of profit which is assumed to be equal to the marginal product of capital will be given by the slopes of the production function at the relevant points.

If the technological change which has raised the production function from OP₁ to OP₂ is to be Harrod-neutral, then slope at point T₁ on production function OP₁ and slope at point T₂ on production function OP₂ must be the same. The slope of functions at T₁ and T₂ would be the same if the tangents drawn at these points are parallel to each other. This is exactly the case in Fig. 8.5 where tangent drawn at point. T₁ on the production function OP₁ before technical change and tangent drawn at point T₂ on production function OP₂ after the technical change are parallel.

Nature of Technological Change and Income Distribution:

In Harrod’s growth model, neutrality of technological progress implies that income distribution between wages and profits will remain constant as equilibrium growth of the economy occurs. In Harrod’s growth model, there are two factors of production-labour and capital – and growth with neutral technological progress causes increase in incomes of both workers and capitalists. Income of workers increase as rate of wages per man hour rises due to increase in their productivity as a result of technological change.

Profits of capitalists increase because they accumulate more capital assets as growth proceeds, though rate of profit per rupee worth of capital remains the same. Thus, commenting on Harrod’s growth model with neutral technological progress Stonier and Hague write, “The workers’ standard of living will rise because his wage rate has risen. The capitalist’s standard of living will rise too but it will do so because he gets much the same rate of return on each pound’s worth of a bigger stock of capital.”

However, if in Harrod’s growth theory capital-saving technological progress occurs, the share of profits in national income will fall and that of wages will rise. On the other hand, if labour-saving technological progress occurs the share of profits in national income will rise and share of wages will decline during the process of growth.