Cost of capital can be defined both from organization’s and investor’s point of view.
From an organization’s point of view, cost of capital is a rate at which an organization raises capital to invest in various projects.
The basic motive of an organization to raise any kind of capital is to invest in its various projects for earning profit. Further, out of that profit, the organization pays interest and dividend to the sources of capital. The amount paid as interest and dividend is considered as cost of capital.
From the investors’ point of view, cost of capital is the rate of return, which investors expect from the capital invested by them in the organization. The calculation of cost of capital is very significant for the management of an organization.
ADVERTISEMENTS:
The significance of cost of capital is as follows:
(a) Capital Budgeting Decision:
Refers to the decision, which helps in calculating profitability of various investment proposals.
(b) Capital Requirement:
ADVERTISEMENTS:
Refers to the extent to which fund is required by an organization at different stages, such as incorporation stage, growth stage, and maturity stage. When an organization is in its incorporation stage or growth stage, it raises more of equity capital as compared to debt capital. The evaluation of cost of capital increases the profitability and solvency of an organization as it helps in analyzing cost efficient financing mix.
(c) Optimum Capital Structure:
Refers to an appropriate capital structure in which total cost of capital would be least. Optimal capital structure suggests the limit of debt capital raised to reduce the cost of capital and enhance the Value of an organization.
(d) Resource Mobilization:
ADVERTISEMENTS:
Enables an organization to mobilize its fund from non-profitable to profitable areas. Resource mobilization helps in reducing risk factor as an organization can shut down its unproductive projects and move the resources to productive projects to earn profit.
(e) Determination of duration of Project:
Refers to evaluating whether the project, for which the capital is raised, is long term or short term. If the project is long term in nature then the organization decides to raise equity capital. However, if the project is short term in nature then the organization determines to raise debt capital.
Cost of capital can be measured by using various methods, as shown in Figure-2:
The explanation of methods measuring cost of capital (as shown in Figure-2) is as follows.
Cost of Debt Capital:
Generally, cost of debt capital refers to the total cost or the rate of interest paid by an organization in raising debt capital. However, in a real situation, total interest paid for raising debt capital is not considered as cost of debt because the total interest is treated as an expense and deducted from tax.
This reduces the tax liability of an organization. Therefore, to calculate the cost of debt, the organization needs to make some adjustments. Let us understand the calculation of cost of debt with the help of an example.
ADVERTISEMENTS:
Suppose an organization raised debt capital of Rs. 10000 and paid 10% interest on it. The organization is paying corporation tax at the rate of 50%. In this ca.se, the total 10% of interest rate would not be deducted from tax and the deduction would be 50% of 10%.
Therefore, the cost of debt would be only 5%. While calculating cost of debt capital, discount allowed, underwriting commission, and cost of advertisement are also considered. These expenses are added to the amount of interest paid, which is considered as total cost of debt capital.
For example, when an organization increases its proportion of debt capital more than the optimum level, then it increases its risk factor. Therefore, the investors feel insecure and their expectations of EPS start increasing, which is the hidden cost related to debt capital.
Formulae to calculate cost of debt are as follows:
ADVERTISEMENTS:
1. When the debt is issued at par
KD = [(1-T)*R]*100
Where,
KD = Cost of debt
ADVERTISEMENTS:
T = Tax rate
R = Rate of interest on debt capital
KD = Cost of debt capital
2. Debt issued at premium or discount when debt is irredeemable:
KD = [1/NP*(1-T)* 100]
Where,
ADVERTISEMENTS:
NP = Net proceeds of debt
3. Cost of redeemable debt:
KD = [{I (1-T) -H (P-NP/N) * (1- T)}/ (P -H NP/2)] * 100
Where,
N = Numbers of years of maturity
P = Redeemable value of debt
ADVERTISEMENTS:
For example, an organization issued 10% debentures of the face value of Rs. 100 redeemable at par after 20 years.
Assuming 50% tax rate and 5% floatation cost, calculate cost of debt in the following conditions:
1. When debentures are issued at par
2. When debentures are issued at 10% discount
3. When debentures are issued at 10% premium
Solution:
ADVERTISEMENTS:
The solution is given as follows:
Cost of redeemable debt = [{I (1-T) + (P- NP/N) (1- T)}/ (P + NP/2)] * 100
1. When debentures are issued at par
KD = [{10(1 – 0.50) + (100 – 95/20) (1 – 0.50)}/ (100 + 95/2)] *100
= 5.25%
2. When debentures are issued at 10% discount
ADVERTISEMENTS:
KD = [{10(1 – 0.50) + (100 – 85/20) (1 – 0.50)}/ (100 + 85/2)] *100
= 5.81%
3. When debenture is issued at 10% premium
KD = [{10(1 – 0.50) + (100 – 110/20) (1 – 0.50)}/ (100 + 110/2)] *100
= 4.52%
Cost of Preference Capital:
Cost of preference capital is the sum of amount of dividend paid and expenses incurred for raising preference shares. The dividend paid on preference shares is not deducted from tax, as dividend is an appropriation of profit and not considered as an expense.
Cost of preference share can be calculated by using the following formulae:
1. Cost of redeemable preference shares:
KP = [{D + F/N (1 – T) + RP/N}/ {P + NP/2}] * 100
Where,
KP = Cost of preference share
D = Annual preference dividend
F = Expenses including underwriting commission, brokerage, and discount
N = Number of years to maturity
RP = Redemption premium
P = Redeemable value of preference share
NP = Net proceeds of preference shares
2. Cost of irredeemable preference shares:
KP = (D/NP) * 100
For example, an organization issues 10% preference shares of Rs. 100 each, redeemable at par after 20 years.
Assuming 4% floatation cost and 50% corporate tax; calculate cost of preference share in the following conditions:
1. When preference shares are issued at par
2. When preference shares are issued at 10% discount
3. When preference shares are issued at 10% premium
Solution:
The solution is given as follows:
Cost of redeemable preference shares = [{(D + F)/N (1 – T) + RP/N}/ {(P + NP)/2}] * 100
1. When preference shares are issued at par:
KP = [{(10 + 4)/20 (1 – 0.50) + 0/20}/ {(100 + 96)/2}] * 100
= 10.30%
2. When preference shares are issued at 10% discount:
KP = [{(10 + 4)/20 (1 – 0.50) + 0/20}/ {(100 + 86)/2}] * 100
= 10.86%
3. When preference shares are issued at 10% premium:
KP = [{(10 + 4)/20 (1 – 0.50) + 0/20}/ {(100 + 106)/2}] * 100
= 9.80%
Cost of Equity Capital:
Calculating the cost of equity capital is a little difficult as compared to debt capital and preference capital. The main reason is that the equity shareholders do not receive fixed interest or dividend. The dividend on equity shares varies depending upon the profit earned by an organization. Risk factor also plays an important role in deciding rate of dividend to be paid on equity capital.
Therefore, there are various approaches to calculate cost of equity capital, as shown in Figure-3:
The explanation of these approaches (as shown in Figure-3) is as follows:
Dividend Price Approach:
The dividend price approach describes the investors’ view before investing in equity shares. According to this approach, investors have certain minimum expectations of receiving dividend even before purchasing equity shares. An investor calculates present market price of the equity shares and their rate of dividend.
The dividend price approach can be mathematically calculated by using the following formula:
KE = (Dividend per share/Market price per share) * 100
KE = Cost of equity capital
However, the dividend price approach is criticized on certain grounds, which are as follows:
a. Does not take into consideration the appreciation in the value of capital. The dividend price approach is based on the assumption that investors expect some dividend on their shares. It completely ignores the fact that some investors also consider the chances of capital appreciation, which increases the value of their shares.
b. Ignores the impact of retained earnings, which affect both the market price of shares and the amount of dividend paid. For example, suppose if an organization keeps major portion of its profit as retained earnings then it would pay low dividend, which may decrease the market price of its shares.
Earnings Price Ratio Approach:
The earnings price ratio approach suggests that cost of equity capital depends upon amount of fixed earnings of an organization. According to the earnings price ratio approach, an investor expects that a certain amount of profit must be generated by an organization.
Investors do not always expect that the organization distribute dividend on a regular basis. Sometimes, they prefer that the organization invests the amount of dividend in further projects to earn profit. In this way, the organization’s profit would increase, which in turn increases the value of its shares in the market.
The formula to calculate cost of capital through the earnings price ratio approach is as follows:
KE = E/MP
Where,
E = Earnings per share
MP = Market price
However, this approach is criticized on the following grounds:
a. Assumes that EPS would remain constant
b. Assumes that market price per share would remain constant
c. Ignores the fact that all the earnings of an organization are not distributed in the form of dividend. However, some part of earnings may be kept in form of retained earnings.
Dividend Price plus Growth Approach:
The dividend price plus growth approach refers to an approach in which the rate of dividend grows with the passage of time. In the dividend price plus growth approach, investors not only expect dividend but regular growth in the rate of dividend. The growth rate of dividend is assumed to be equal to the growth rate in EPS and market price per share.
In the dividend price plus growth approach, cost of capital can be calculated mathematically by using the following formula:
KE = [(D/MP) + GJ * 100
Where,
D = Expected dividend per share, at the end of period
G = Growth rate in expected dividends
This approach is considered as the best approach to evaluate the expectations of investors and calculate the cost of equity capital. For example, your company’s share is quoted in the market at Rs. 20 currently. The company pays as dividend of Re. 1 per share and the investor’s market expects a growth rate of 5% year.
a. Compute the company’s equity cost of capital.
b. If the anticipated growth rate is 6% p.a., calculate the indicated market price per share.
c. If the company’s cost of capital is 8% and the anticipated growth rate is 5% p.a., calculate the indicated market price if the dividend of Re. 1 per share is to be maintained.
Solution:
The equity cost of capital is as follows:
a. KE = [{D/MP) + G] * 100
= [(1/20) + 0.05] * 100= 10%
b. MP = [{D + (G * MP)}/KE] * 100 = [{1 + (0.06 * MP)}/0.10] * 100 = Rs. 16.94
c. MP = [{D + (G * MP)}/KE] * 100 = [{1 + (0.05 * MP)}/0.08] * 100 = Rs. 20.32
Realized Yield Approach:
In the realized yield approach, an investor expects to earn the same amount of dividend, which the organization has paid in past few years. In this approach, the growth in dividend is not considered as major factors for deciding the cost of capital.
This approach is based on the following assumptions:
a. Risk factor remains constant in an organization. Returns in the given risk remain the same as per the expectations of shareholders.
b. Realized yield is equivalent to the reinvestment opportunity rate for shareholders.
According to the realized yield approach, cost of capital can be calculated mathematically by using the following formula:
KE = [{(D-P)/p} – 1] * 100
Where,
P = Price at the end of the period,
p = Price per share to day
Capital Asset Price Model (CAPM):
CAPM helps in calculating the expected rate of return from a share of equivalent risk in the capital market. The cost of shares that carry risk would be equal to cost of lost opportunity. For example, an investor has two investment options- to buy the shares of either X Ltd. or Y Ltd. If the investor decides to buy the shares of X Ltd. then the cost of shares of Y Ltd. would be the cost of lost opportunity.
CAPM is based on the following assumptions:
a. A rationale investor would always avoid risk
b. A rationale investor would always wish to maximize the expected yield
c. All investors would have similar expectations
d. All investors can lend freely on the riskless rates of return
e. Capital market is in good condition and there is no existence of tax
f. Capital market is competitive in nature
g. Securities are completely divisible and there is no transaction cost
The computation of cost of capital using CAPM is based on the condition that the required rate of return on any share should be equal to the sum of risk less rate of interest and premium for the risk.
According to CAPM, cost of capital can be calculated mathematically by using the following formulae:
E = R1 +β {E (R2) – R1}
Where,
E = Expected rate of return on asset
β = Beta coefficient of assets
R1 = Risk free rate of return
E (R2) = Expected return from market portfolio
This value can be calculated by analyzing data of usually five years.
Formula used to calculate beta value is as follow:
β = PIM (SD1) (SDM)/SD2M
Where,
β = Beta of stock
PIM = Correlation coefficient between the returns on stock, I and the returns on market portfolio, M.
SD1 = Standard deviation of returns on assets
SDM = Standard deviation of returns on the market portfolio
SD2M = Variance of market returns
Bond Yield plus Risk Premium Approach:
The bond yield plus risk premium approach states that the cost on equity capital should be equal to the sum of returns on long-term bonds of an organization and risk premium given on equity shares. The risk premium is paid on equity shares because they carry high risk.
Mathematically, the cost of capital is calculated as:
Cost of equity capital= Returns on long-term bonds + Risk premium
The bond yield plus risk premium approach is based on the fact that a risky organization would have high financial leverage. As a result of this, it would be earning higher profit. Therefore, the equity shareholders due to higher risks on their investments expect higher returns in the form of risk premium.
Gordon Model:
The Gordon model was proposed by Myron Gordon to calculate cost of equity capital. As per this model, an investor always prefers less risky investment as compared to more risky investment.
Therefore, an organization should pay risk premium only on risky investment. The Gordon model also suggests that an investor would always prefer more of those investments, which would provide them current income.
The Gordon model is based on the following assumptions:
a. The rate of return on the investments of an organization is constant
b. The cost of equity capital is more than the growth rate
c. The corporation tax does not exist in the economy
d. The organization has perpetual existence
e. The growth rate of the organization is a part of retention ratio and its rate of return
According to the Gordon model, cost of capital can be calculated mathematically by using the following formula:
P = E (1 -b)/K – br
Where,
P = Price per share at the beginning of the year
E = Earnings per share at the end of the year
b = Fraction of retained earnings
K = Rate of return required by shareholders
r = Rate of return earned on investments made by the organization
For example, assume that the organization pays the corporation tax at the rate of 50%.
Compute after tax cost of capital in the following cases:
a. 10% preference shares sold at par.
b. Irredeemable debentures sold at par at the interest rate of 10%.
c. Redeemable debentures of Rs. 100 each, sold at Rs. 95 carrying 8% interest rate. The maturity period of debentures is after 10 years.
d. Equity shares sold at market price of Rs. 100 and paying a current dividend of Rs. 10 per share. The expected growth in the dividend of the share is 8%.
Solution:
The solution is given as follows:
a. The cost of preference shares after tax is 10%
b. Cost of debt for irredeemable debenture when issued at par = [(1 – T) * R] * 100
KD = [(1 – 0.50) * 10%)] * 100
= 5%
c. Cost of redeemable debenture = [{I (1-T) + (P – NP/N) (1- T)}/ (P + NP/2)] * 100
KD = [{8(1 – 0.50) + (100 – 95/10) (1 – 0.50)}/ (100 + 95/2)] * 100
= 4.61%
d. Cost of equity share when growth rate of dividend is given = [(D/MP) + G] * 100
KE = [(10/100) + 8%J * 100
= 18%
Cost of Retained Earnings:
Retained earnings are organizations’ own profit reserves, which are not distributed as dividend. These are kept to finance long-term as well as short-term projects of the organization. It is argued that the retained earnings do not cost anything to the organization. It is debated that there is no obligation either formal or implied, to earn any profit by investing retained earnings.
However, it is not correct because the investors expect that if the organization is not distributing dividend and keeping a part of profit as reserves then it should invest the retained earnings in profitable projects. Further, the investors expect that the organization should distribute the profit earned by investing retained earnings in the form of dividend.
Cost of retained earnings can be calculated with the help of various approaches, which are as follows:
(a) KE = KR Approach:
Assumes that if the profit earned by an organization is not retained but is distributed as dividend, then the shareholders would invest this dividend in other projects to earn further profit. If an organization retains the dividend then it prohibits the shareholders from earning more profit.
Therefore, for retaining the dividend, the organization should earn the profit, which the shareholders would have earned by investing the dividend in other projects. Therefore, the amount of profit expected from the organization on retained earnings is the cost of retained earnings.
(b) Soloman Erza Approach:
Includes the two options that an organization has that is either to retain the earnings to meet future uncertainties or invest in its or other organization’s projects.
Weighted Average Cost of Capital:
Weighted average cost of capital is determined by multiplying the cost of each source of capital with its respective proportion in the total capital. Let us understand the concept of weighted average cost of capital with the help of an example. Suppose an organization raises capital by issuing debentures and equity shares.
It pays interest on debt capital and dividend on equity capital. When the organization adds the total interest paid on debt capital to the total dividend paid on equity capital, it obtains weighted average cost of capital. An organization requires to generate the profit on its various investments equal to the weighted average cost of capital.
Weighted average cost of capital can be calculated mathematically by using the following formula:
Weighted Average Cost of Capital = (KE * E) + (KP * P) + (KD * D) + (KR * R)
Where,
E = Proportion of equity capital in capital structure
P = Proportion of preference capital in capital structure
D = Proportion of debt capital in capital structure
KR = Cost of proportion of retained earnings in capital structure
R = Proportion of retained earnings in capital structure
Let us understand the weighted average cost of capital with the help of some examples.
Example-1:
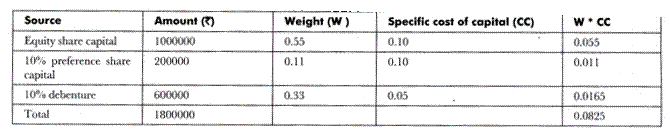
ABC Ltd. has the following capital structure on 31st March 2008:
Equity shares (10000 shares issued) = Rs. 1000000
10% preference shares = Rs. 200000
10% debentures = Rs. 600000
The shares of the organization are currently sold at Rs. 100. It is expected that the organization would provide dividend of Rs. 10 per share, which would grow at the rate of 10% forever. Assuming 50% corporate tax rate, calculate weighted average cost of capital on existing capital structure.
Solution:
The solution is given as follows:
Cost of debt after tax = [(1 – T) * R] * 100
KD = [(1-0.50)* 10%] * 100
= 5%
Cost of equity capital when growth rate is given = [(D/MP) + G] * 100
KE = [(10/100) + 10%]* 100
= 10%
Calculation of weighted average cost of capital is shown as follows:
Therefore, weighted average cost of capital = 0.0825
Example-2:
A fan manufacturing organization wishes to determine the weighted average cost of capital to evaluate capital budgeting projects.
You have been given the following information:
Additional Information:
a. 10 years 10% debentures of? 1000 face value, redeemable at 10% premium can be sold at par, 5% floatation costs.
b. 10% preference shares of selling price Rs. 1000 per share and 5% floatation costs
c. Equity shares of selling price Rs. 100 per share with Rs. 10 floatation cost per share
The corporate tax is 50% and expected growth in equity dividend is 20% per year. The expected dividend at the current financial year is Rs. 10 per share. You are required to calculate the weighted average cost of capital.
Solution:
The solution is given as follows:
Cost of debt capital = [{I (1-T) + (P – NP/N) (1-T)}/ (P + NP/2)] * 100
KD =[ 1(100 (1 – 0.50) + (1100 – 950/10) (1 – 0.50))/ (1100 + 950/2)1 ]* 100
= 5.6%
Cost of preference share = (D/NP) * 100
KP = {10/ (1000 – 50)} * 100
= 1.05%
Cost of equity capital = [(D/MP) + G] * 100
KE = 1(10/100) + 0.20) * 100
= 30%
Therefore, weighted average cost of capital is = 15.024%
Example-3:
The following is the capital structure of Saras Ltd. As on 31-12-2005:
The market price of the company’s share is Rs. 110 and it is expected that a dividend of Rs. 10 per share would be declared after one year. The dividend growth rate is 6%.
a. If the company is in the 50% tax bracket, compute weighted average cost of capital.
b. Assuming that in order to finance an expansion plan, the company intends to borrow a fund of Rs. 20 lakhs bearing 14% rate of interest, what will be the company’s revised weighted average cost of capital? This financing decision is expected to increase dividend from Rs. 10 to Rs. 12 per share. However, the market price of equity share is expected to decline from Rs. 110 to 105 per share.
Solution:
The solution to the given problem is as follows:
a. KE = [(D/MP) + G]* 100
= [(10/110) + 0.06] *100 = 15.09
KD = [(1 – T) * R] *100
= [(1-0.50)* 0.12]* 100 = 6%
KP = 10%
a. KE = [(D/MP) + G]*100
= [(12/105) + 0.20J * 100 = 31.42
KD = [(1-T)*R]*100
= [(1-0.50) * 0.14] * 100 = 7%
Marginal Cost of Capital:
Marginal cost of capital can be defined as the cost of additional capital required by an organization to finance the investment proposals. It is calculated by first estimating the cost of each source of capital, which is based on the market value of the capital.
After that, it is identified that which source of capital would be more appropriate for financing a project. The marginal cost of capital is ascertained by taking into consideration the effect of additional cost of capital on the overall profit. In simpler terms, the marginal cost of capital is calculated in the same manner as the weighted average cost of capital is calculated by just adding additional capital to the total cost of capital.
Marginal cost of capital can be calculated mathematically by using the following formula:
Marginal Cost of Capital = KE {E/ (E + D + P + R)} + KD {D/ (E + D + P + R)} + KP (P/ (E + D + P R)} + KR {R/ (E + D + P + R)}
For example a company has equity shares of Rs. 100 each, 10% preference shares, and 12% debentures in the proportion of 3:2:5. The company needs further capital that is available from a financial institution @ 14% interest. The new proportion would be 3:2:5:5 for equity capital, preference capital, debentures, and loans from financial institutions, respectively.
The company pays 40% tax on income. The market price of equity shares is Rs. 120 per share. Expected dividend at the end of the year is Rs. 6 per share. Dividends are expected to grow every year @ 5%. How will the cost of capital change on borrowing funds from financial institutions?
Solution:
The calculations of equity and debt capital are as follows:
KE = [(D/MP) + G] *100
= [(6/120) + 0.0.05] * 100 = 10%
KD = [(1-T) *R] * 100
= [(1 – 0.40)* 0.121 * 100
= 7.2%
Cost of loan raised from bank, KD = [(1 – T) * R] * 100
= [(1-0.40) * 0.12] * 100 = 8.4
Therefore it can be analyzed from the calculation that the cost of capital decreases on borrowing funds from the financial institution. Before borrowing loan from the financial institution, cost of capital was 0.086, which reduced to 0.083 after borrowing.