Techniques of Capital Budgeting under Certainty Conditions

Certainty refers to the condition in which the investors are aware about market.

In certainty condition, investor knows about various factors, such as opportunities to invest, cost incurred in investment and the expected return from every investment.

The investment decisions regarding a project are concerned with the profitability and selection of a project. Investment decisions involve new investment, replacement, and deepening of capital.

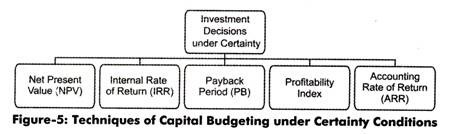
Figure-5 shows some of the most commonly used methods for investment decisions under certainty conditions:

The techniques for capital budgeting (as shown in Figure-5) are discussed in detail below.

1. Net Present Value Method:

NPV is one of the most widely used methods of evaluating capital budgeting. This method is also used to evaluate the profitability of a project. As the name suggests, NPV is the difference between the present value of cash inflows and cash outflows in a given project.

The formula to calculate NPV is as follows:

NPV = C₁ / (1+r) + C₂ / (1+r) ² + C₃ / (1+r) ³ + ……. + C_n / (1+r) ⁿ – l₀

NPV= ∑ⁿ_t=1C_t/ (1+r) ⁿ –I₀

Where,

C_t = Net cash received at the end of year t

I₀ = Initial investment outlay

r = Discount rate/the required minimum rate of return on investment in a project

n = Time Duration of the project (in years)

Figure-6 shows the steps involved in calculating the NPV of a project:

The steps of calculating NPV (as shown in Figure-6) are explained as follows:

1. Forecasting cash flows:

Involves estimating the cash inflows and cash outflows in the specified duration of the project. An accurate estimation of cash flows helps in determining the actual profitability of the project.

2. Estimating required rate of return:

Involves determining the required rate of return on a project al which the present value of a cash flow is calculated. Generally, the opportunity cost of the capital is assumed as the required rate of return.

3. Calculating the present value of cash flows:

Refers to the third step of calculating NPV in which the discount rate is used to find out the present value of cash inflows and cash outflows.

4. Finding out NPV:

Indicates the final step of calculating NPV. The NPV of a project is determined by subtracting the present value of cash outflows from the present value of cash inflows. A project should be accepted if -Ls NPV is positive (NPV>0) and rejected if its NPV is negative (NPV<0). An organization may or may not accept the project if it is NPV is equal to zero.

The rule of thumb for accepting or rejecting a project according to the NPV method is shown in Table-3:

Following are the advantages of using the NPV method:

(a) Accurate Profitability Measurement:

Provides exact profitability measures of a project by taking into account all cash flows that occur throughout the life-time of a project. The NPV method also considers the TVM factor while determining the profitability of a project.

The accurate measurement of the profitability of a project helps in maximizing the shareholders wealth.

(b) Value-additively:

Refers to one of the main advantage of the NPV method. The principle of value-additively implies that the present value of a number of cash flows is the total of the present value of individual cash flows. For example, u e can determine the present value of an annuity by using its direct formula or by calculating the present value of each independent cash flow and summing up those present values together. This helps in simplifying the procedure of calculating the present values of uneven cash flows.

NPV is one of the most effective methods for capital budgeting, which, in turn, helps in efficient selection of a project. However, there is a significant drawback of this method as it is based on forecasting cash flows occurring throughout the course of a project. In real life, forecasting cash flows is a difficult process.

2. Internal Rate of Return Method:

IRR is one of the time-based methods to analyze the capital investment decisions, which helps in selecting profitable projects. The internal rate of return is the discount rate that makes the NPVs of all cash flows arising out of any project, equal to zero. The term internal denotes that this method does not take into account external factors, such as inflation. In more simplified terms, IRR denotes the interest rate at which the NPVs of all expenses made on a project (cash outflow, equals to the NPVs of all benefits or income arising out of the project (cash inflow).

Let us consider the following example:

XYZ organization is planning to start a new project. The total cost of the project is Rs. 20000 at present and the project is expected to give returns of Rs. 12000, Rs. 10000, and Rs. 8000 at the end of the first, second, and third year, respectively. Let us assume that the discount rate r will make NPV of the project, equal to zero.

Therefore, 12000/ (1+r) +10000/ (1+r) ² +8000/ (1+r) ³ – 20000 =0

Where, r= IRR of the project

If we determine r by solving the equation, we can find out the IRR of the project, which would make the NPV of the project equal to zero.

If the IRR of the project is greater than the cost of capital of the project, the project is accepted. However, a project must be rejected, if the IRR of the project is less than the cost of capital of the project. In this method, the profitability of a project is represented as a percentage, which is very easy to compare with the cost of capital.

Some of the other advantages of the IRR method are as follows:

a. Provides the accurate measurement of profitability of a project by considering all cash inflows and outflow generated throughout the duration of the project

b. Takes the TVM factor into consideration, which helps in determining the exact profitability of the project

c. Helps in maximizing the wealth of shareholders

However, there are certain disadvantages of the IRR method.

Some of the main disadvantages of the IRR method are as follows:

(a) Different Rates of Returns:

Refer to the fact that the IRR method may calculate multiple rates of returns for which the NPVs of all cash flows would become equal to zero. In such cases, it is difficult for the project manager to select a particular rate from the multiple rates, which results in complexity in the project selection process.

(b) Value-additivity:

Refers to one of the main limitation of the IRR method. Unlike in the NPV method, the value additivity principal is not applicable in the IRR method.

3. Payback Period Method:

Payback period is a traditional method of evaluating investment in a project. The payback period is the duration of time taken to recover the initial cost of a project. The payback period method is easy and quantitative in approach and does not take the TVM factor into account.

The basic principle of the payback period method is that if the initial cost of a project is recouped in a shorter period of time, the project is said to be profitable. Different projects can be ranked according to the length of the payback period. The projects with shorter payback period are ranked higher than the projects with longer payback period.

Generally, payback period is expressed in years and can be calculated by using the following formula:

Payback Period = Investment required for the project/ Net annual return or cash inflow

Let us consider the following example:

A project involves an initial cost of Rs. 120000 and is expected to yield a return of Rs. 15000 every year for a period of 15 years. The payback period of the project would be 120000/15000= 8 years. Therefore, it can be said that the initial investment of the project, which is Rs. 120000, would be recouped in eight years.

The payback period method is very objective and simple in nature; therefore it saves time and cost. This method is also useful in measuring the liquidity of a project as it shows the time period in which the initial cost of a project is recouped.

In addition, the payback period method helps project managers to easily make project selection decisions. However, the main limitation of this method is that it does not take the TVM factor; therefore, the exact profitability of the project is not measured.

4. Profitability Index:

Profitability Index refers to a ratio of the present value of cash inflow to the present value of cash outflow. Profitability index is very similar to the NPV method as it also measures the difference between cash inflow and cash outflow in an organization.

The mathematical formula to calculate profitability index is as follows:

Profitability Index= Present value of cash inflow/Present value of cash outflow

The profitability index should be greater than one for the selection of a project. The profitability index method is based on the time value of money and is intended to maximize the wealth of the shareholders. It is used to measure the relative cash surplus of an organization by comparing the cash inflow and outflow.

5. Average Rate of Return Method:

ARR is also known as Accounting Rate of Return or Return on Investment (ROI). It is also a traditional method to evaluate investment on a project. This method is significantly different from the other methods of project selection as it deals with the accounting profit of a project rather than the cash flows. It does not take into account the time period involved in determining the rate of return of a cash flow.

The mathematical formula to calculate ARR is as follows:

ARR = Average Income/Average Investment * 100

In this equation, the average income is defined as Earnings before Interest and after Taxes [EBIT (I-T)] and the average investment is calculated as follows:

Average Investment = (book value at the beginning of the project + book value at the end of the project life)/2

EBIT refers to the gross profit from a project before paying interest on capital and taxes.

Let us consider some examples for calculating ARR.

Example-1:

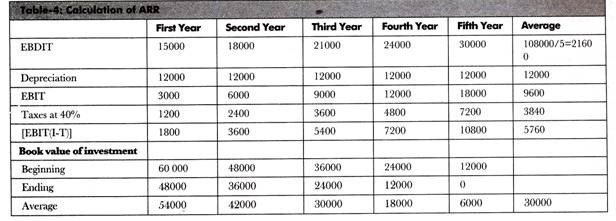
A project cost Rs. 60000 to an organization. The project is expected to provide Earnings before Depreciation, Interest and Taxes (EBDIT) of Rs. 15000, Rs. 18000, Rs. 21000, Rs. 24000, and Rs. 30000 every year for five years. Suppose the depreciation is on straight line basis and the rate of interest is 40%. Calculate the ARR for the project.

Solution:

The calculation of ARR of the project is shown in Table-4:

Therefore, the ARR = (5760/30000) × 100 = 19.2%

Different projects can be ranked on the basis of their ARR. The project with the highest ARR should be ranked the highest and the project with the lowest ARR should be ranked the lowest. The main advantage of the ARR method is that it makes the use of accounting data; therefore, the project manager needs not to estimate independent cash flows.

However, this method considers accounting profit instead of cash flows while evaluating the profitability of a project. The accounting profit also includes non-cash items; therefore, it is not appropriate to accept or reject a project on the basis of the accounting profit. Moreover, the ARR method does not take the TVM factor into account. In such a case, the profitability measured, does not reflect the real worth of a project.

Example-2:

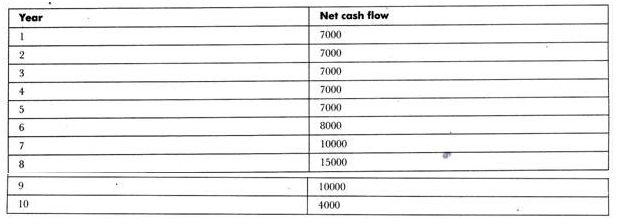
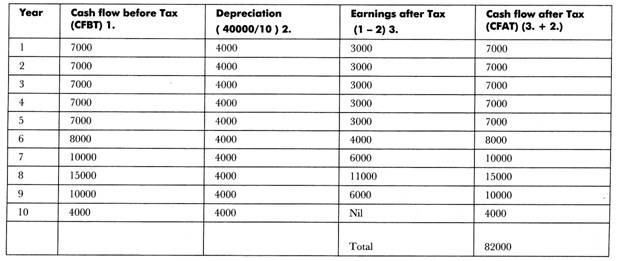
A company has an investment opportunity costing Rs. 40000 with the following expected net cash flow after taxes and before depreciation:

Using 10% as the cost of capital determine the following:

a. Payback period

b. Net present value at 10% discount factor

c. Profitability index at 10% discount factor

d. Internal rate of return with the help of 10% and 15% discount factor.

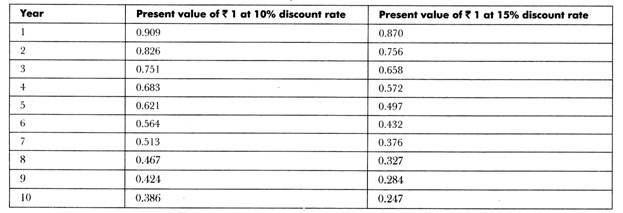
The present value of Rs. 1 at 10% and 5% discount rate for ten years are as follows:

Solution:

The solution to the given problem is as follows:

Opportunity cost of investment = Rs. 40,000.

Determination of cash flow after the taxes:

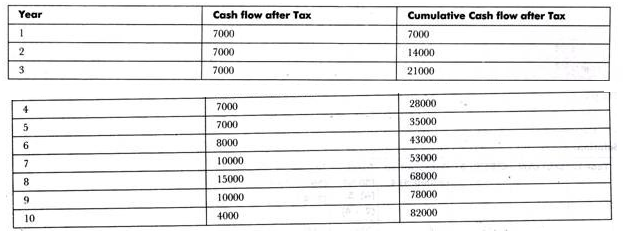
a. Payback period would be calculated as follows:

The preceding table shows that the opportunity cost would be recovered between the fifth and sixth year. Therefore, the payback period would be five years and a part of the sixth year.

The value would be 5 + 5000/8000 = 5 + 0.625 = 5.625 years.

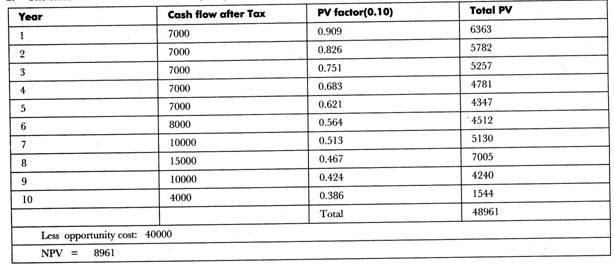
b. The calculation of Net Present Value (NPV) of cash flow at 10% discount factor is shown in the following table:

c. Profitability index at discount factor of 10% would be:

PI = (48961 / 40000)* 0.10 = 48961 / 36000 = 1.360.

d. Internal Rate of Return (IRR) would be calculated as follows:

The payback period is 5.625 and by referring to the table we find that discount factor closest to 5.625 for 10 years is 5.650 (12% of interest) and 5.426 (13% of interest). The actual value of internal rate of return would lie between 12% and 13%.

It would be calculated as:

= 12 + (5.650-5.625 / 5.650-5.426) = 12 + (0.025 / 0.224) = 12 + 0.111 = 12.111

Therefore, the required rate of return of project would be 12.111%.

Example-3:

X Co. Ltd. is considering two mutually exclusive projects.

The following are the information for the same:

The net cash inflows before the tax and depreciation are:

The project would depreciate on straight line method.

You are required to calculate:

a. The net present value and profitability index for each project.

b. The internal rate of return for each project. Which project would be selected and why?

Solution:

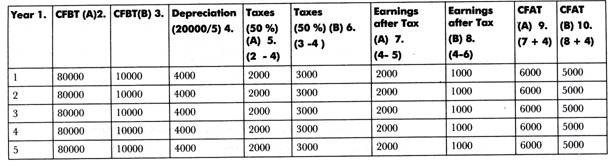
The determination of cash flow after the taxes in the case of project A and B:

a. The Net Present Value (NPV) would be calculated as follows:

b. The profitability index would be calculated as follows:

Profitability index for project A = 22388 / 20000 = 1.119

Profitability index for project B = 18665 / 20000 = 0.933

The Internal Rate of Return (IRR) of the project would be calculated as follows:

The payback period for the project A would be 3 + 4398 / 6000 = 3 + 0.733 = 3.733

By referring to the table, we find that the discount factor closest to 3.733 for five years is 3.791 (10% of interest) and 3.696 (11% of interest). The actual value of internal rate of return would lie between 10% and 11%. It would be calculated as

= 10 + (3.791-3.733 / 3.791-3.696) = 10+ (0.058 /0.095) = 10 + 0.611 = 10.611

Therefore, the required rate of return of project A would be 10.611%.

The payback period for the project B would be 3 – 665 / 6000 = 3 – 0.110 = 3.110

By referring to the table, we find that discount factor closest to 3.110 for five years is 3.127 (18% of interest) and 3.058 (19% of interest). The actual value of internal rate of return would lie between 18% and 19%.

It would be calculated as:

= 18 + (3.127-3.110 / 3.127-3.058) = 18+ (0.017 /0.069) = 18 + 0.246= 18.246

Therefore, the required rate of return of project B would be 18.246%.

The project A would be selected because of the following reasons:

The NPV in case of project A is positive while in case of project B is negative.

Also, the profitability index in case of project A is greater than zero in the case of project B.

Example-4:

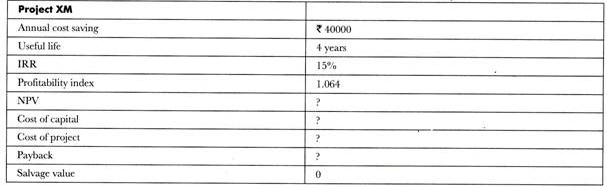
Following are the data on a capital project being evaluated by the management of the company:

Find the missing values considering the following table of discount factor only.

Solution:

The given annual cost saving is Rs. 40,000 for the useful life of four years at IRR of 15%.

The Net Present Value (NPV) at 15% discount factor is shown in the following data:

Profitability index = Present value of cash inflow / Present value of cash outflow

Or, 1.064 = 128280 / PV of cash outflow

Or, present value of cash outflow = 128280 / 1.064 = 120564 ——–equation (1)

Therefore, the cost of the project would be Rs. 120564.

From equation (1)

NPV = present value of cash inflow – present value of cash outflow

= 128280- 120564 = 7716.

Payback period would be calculated as follows:

The initial investment or cost of the project would be recovered between third and fourth years. Therefore, the payback period would be three years and a part of fourth year.

= 3 + 8280 / 40000 = 3 + 0.207 = 3.207

Example-5:

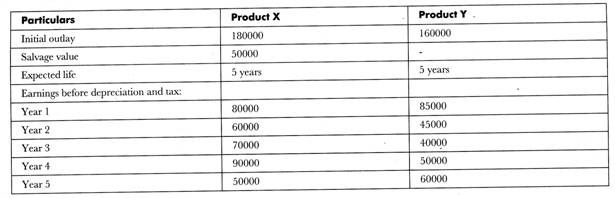
The following are two projects being considered by the company:

Cost of capital is 10% and tax rate is 50%.

Find:

a. Net cash flow

b. Which project is to be purchased under?

I. Payback period method

II. NPV method

III. IRR method

Solution:

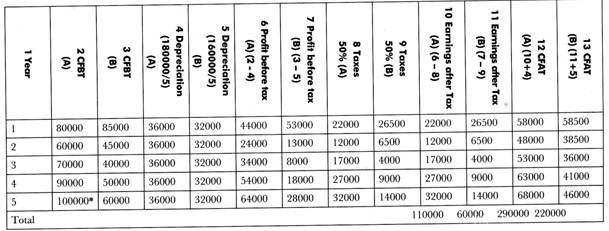
The determination of cash flow after the taxes in the case of project A and B:

a. Net cash flow = Net cash inflow – Net cash outflow

In case of project A = 290000 – 180000 = 110000

In case of project B = 220000 – 160000 = 60000

b. (i) Calculation of payback period method:

Payback period method in case of project A:

The initial investment would be recovered between third and the fourth year. Therefore, the present value would be recovered in the third year and a part of the fourth year.

= 3 + 21000 / 63000 = 3 + 0.33 = 3.33

Payback period method in case of project B:

The initial investment would be recovered between the third and fourth year. Therefore, the present value would be recovered in the third year and a part of the fourth year.

= 3 + 27000 / 41000 = 3 + 0.66 = 3.60

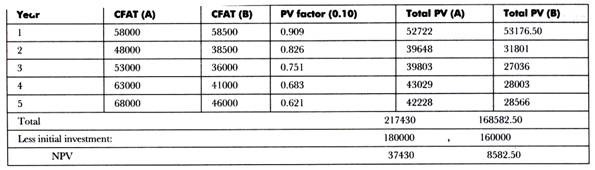
(ii) The Net Present Value (NPV) would fee calculated as follows:

(iii) IRR would be calculated as follows:

IRR in case of project A:

Payback period of project A is 3.333 and by referring to the table, we find that the discount factor closest to 3.333 for five years is 3.352 (15% rate of interest) and 3.274 (16% rate of interest). The actual value of internal rate of return would lie between 15% and 16%.

It would be calculated as:

= 15 + (3.352-3.333 / 3.352-3.274) = 15 + (0.019 / 0.078) = 15 + 0.243 = 15.243

IRR in case of project B:

Payback period of project A is 3.60 and by referring to the table, we find that the discount factor closest to 3.60 for five years is 3.605 (12% of interest) and 3.517 (13% of interest). The actual value of internal rate of return would lie between 12% and 13%.

It would be calculated as:

= 12 + (3.605-3.600 / 3.605-3.517) = 12 + (0.005 / 0.088) = 12 + 0.057 = 12.057