Golden Rule of Capital Accumulation | Economic Growth

Let us make an in-depth study of the Golden Rule of Capital Accumulation. After reading this article you will be able to learn about: 1. Meaning of Golden Rule of Capital Accumulation 2. Determining the Golden Rule Level of Capital 3. Condition for the Golden Rule of Accumulation 4. Explanation of the Condition 5. Importance of Saving in the Context of the Golden Rule.

Meaning of Golden Rule of Capital Accumulation:

The Solow model shows at least one thing very clearly — how an economy’s rate of saving and the level (volume) of investment conjointly determine its steady-state levels of capital and income.

But higher saving rate is not always a good thing.

The aim is more consumption and improved living standards of the people. So every society has to take decision regarding optimal consumption and saving (capital formation).

Thus, pushing the saving rate to higher and higher levels is not always desirable. If, in an extreme situation, an economy saves its entire income, and there is no consumption, economic welfare, instead of rising, will fall. We can now use the Solow model to find out the optimal level of capital of a society which maximises the economic well-being of its members in terms of consump­tion spending.

The reason is that consumption is a measure of welfare, not saving or accumulation of capital. Saving is not an end in itself, but a means to an end.

No doubt, by fixing the saving rate, the policymakers can determine the economy’s steady state. And if the objective of economic policy is maximisation of social welfare, it is in the rightness of things for the policymakers to choose the steady state with the highest level of consumption.

The steady-state, value of k which maximises consumption per worker is called the Golden Rule Level of Capital, a term first coined by Edmund Phelps and is denoted by k*_g.

Determining the Golden Rule Level of Capital:

In order to ascertain whether the economy is at the Golden Rule level, we have to determine first the steady-state consumption per worker. Then we can find out which steady state provides the maximum consumption per worker.

Since consumption (c) is the difference between output (y) and investment (i), for finding steady-state consumption, we have to substitute steady-state values for output and investment. Steady-state output per worker is f(k*), where k* is the steady-state capital stock per worker.

Moreover, in a steady state since capital stock is not changing, investment is equal to depreciation. If we substitute f(k*) for y and δk* for i, we can express steady-state consumption per worker as

c* = f(k*) – δk*. …(17)

Equation (17) suggests that steady-state consumption is what is left of steady-state output after making provision for steady-state depreciation. This equation makes one point quite clear—an increase in steady-state capital has two opposite effects on steady-state consump­tion.

One is favourable, the other is not. On the positive side, more capital means more output. On the negative side, more capital also means that more output must be used to replace worn- out capital.

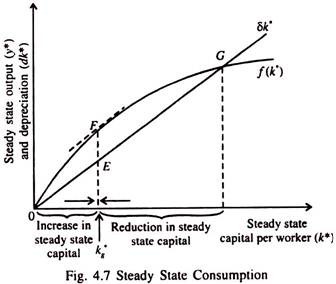
In Fig. 4.7 we show steady-state output and steady-state depreciation as a function of the steady-state capital stock. Steady-state consumption is the difference between output and depreciation. From this figure it is clear that there is only one level of capital stock — the Golden Rule level of k* — that maximises consumption.

The most important point which should not be missed while compar­ing steady states is that higher levels of capital affect both output and de­preciation. If actual capital stock is less than the Golden Rule level, an increase in capital stock raises output faster than depreciation. As a result consumption rises.

In such a situation, the production function f(k*) is steeper than the steady-state deprecia­tion line (δk*). This means that the gap is vertical distance between the two curves — which equals consump­tion per worker — grows as k* in­creases. On the other hand, if the actual capital stock exceeds the Golden Rule level, an increase in the capital stock reduces consumption.

The reason for this is that the increase in output is smaller than the increase in depreciation. In such a situation the production function is flatter than the δk* line. So the gap between the two curves — which measures the level of consumption — falls as k* rises.

At the Golden Rule level of capital, the production function and the line of depreciation have the same slope, this implies that consumption is at the highest possible level.

Condition for the Golden Rule of Accumulation:

The Golden Rule level of capital is characterised by a simple condition. Since at the Golden Rule level of capital (k*) the slope of both the production function (i.e., the MPK) and the depreciation line (i.e., δ) are equal, we have

MPK = δ …(18)

Equation (18), which describes the Golden Rule, simply implies that at k*, the MPK is equal to the rate of depreciation.

Explanation of the Condition:

Suppose an economy is having some steady-state capital stock k* and the government is planning to increase the capital stock by one unit to k* + 1 through some policy measure. The extra output that can be obtained from this extra capital Δk isf(k*+ 1 )-f(k*), which is indeed the MPK.

The amount of extra depreciation due to the increase in the stock of capital is 8. So the net effect of this extra unit of capital on consumption is then MPK – δ. If MPK – δ > 0, then increase in capital increases consumption.

This implies that k* has to be below the Golden Rule level. If MPK- δ < 0, exactly the opposite will happen. In this case, an increase in capital decreases consumption and k* must lie above the Golden Rule level.

Thus the Golden Rule of capital accumulation is described by the following condition:

MPK –δ = 0 … (19)

This means that at k*, MPK, net of depreciation, is zero. This condition can be used by a policy-maker for finding out the capital stock for an economy which maximises the level of consumption, i.e., the so-called Golden Rule capital stock.

It is very easy to derive the Golden Rule. We know that c* = f(k*) – δ k*. To find the k* which maximises c*, we have to differentiate c* with respect to k*, i.e., dc*/dk* = f'(k*) – δ and set this equal to zero, i.e., f'(k*) – δ = 0 or f(k*) = δ. Here f'(k*) is the MPK. Thus we get the Golden Rule condition of the Solow growth model.

Importance of Saving in the Context of the Golden Rule:

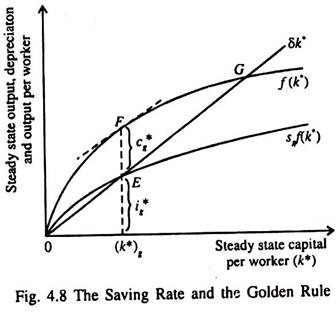
It may be noted that an economy does not automatically move toward the ideal situation, that is, the Golden Rule steady state. For attaining any particular steady-state capital stock adequate saving must be generated. Fig. 4.8 shows the steady-state saving rate used to generate the Golden Rule level of capital.

If the actual saving rate exceeds the rate (s_g) shown in Fig. 4.8, the steady-state capital stock will be excessive. In contrast, if the saving rate is lower than s_g the steady-state capital stock will be inadequate. In either case, steady-state consumption level will be less than it is at the Golden Rule steady state.

Thus to reach the Golden Rule steady state the economy’s saving rate has to be appropriate — neither too much, nor too less. In other words, there is only one saving rate which generates the Golden Rule levei of capital (k*_g).

Any change in the. rate of saving would shift the saving curve sf(k) and would move the economy to a different steady state in which the consumption level would be less than it was in the original steady state.

Theory and Practice:

So there are two ways of finding out the Golden Rule steady state — looking at steady- state consumption or looking the MPK, Both the methods yield the same result. So the routes are different but the destination is the same.

Since estimates of MPK are readily available the second method is more convenient for finding out whether an economy is
currently at, above, or below its Golden Rule capital stock.

But information (estimates) about steady-state consumption at alternative savings rate is (are) not readily available. This is why the first method is not normally used for practical purposes.

Impact of Changes in Propensity to Save:

Since saving is so important for the growth process, we may consider the impact of changes in saving propensity on the growth rate. Here we consider two situations: (i) one in which the economy starts with more capital than in the Golden Rule steady state and (ii) one in which it starts with less capital than in the Golden Rule situation. These two cases present two different problems from the point of view of policy-making.

Situation 1:

Starting with excessive capital:

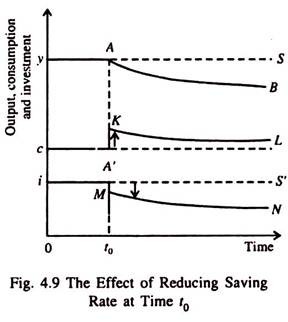
If an economy starts with a steady state with more capital than it would have in the Golden Rule steady state, the appropriate course of ac­tion for the policymakers would be to reduce the saving rate in order to reduce the stock of capital.

Let us suppose, as shown in Fig. 4.9, that these policies succeed and at some point (say t₀) the saving rate falls to such a level that, ultimately, the Golden Rule steady state is reached. We may now examine the effect of a fall in saving on output consumption, and investment.

In Fig. 4.9 we see that the immediate effect of a fall in the saving rate (at time t₀) is to increase consumption and an equal fall in investment. With the passage of time, with a fall in the stock of capital all the three variables, viz., output, consumption and investment, fall together. This point requires a little elucidation.

The fall in saving rate causes an immediate increase in consumption and a fall in investment. Since investment and depreciation were equal in the initial steady state, invest­ment will now fall short of depreciation. This simply means that the economy is not in a steady state any more.

The capital stock gradually falls, leading to fall in output, consumption and investment. All the three variables continue to dwindle until the economy reaches the new steady state. Since the new steady state is assumed to be the Golden Rule steady state, consumption must be higher than it was before the change in the saving rate, even though y and i are lower.

Situation 2:

Starting with inadequate capital:

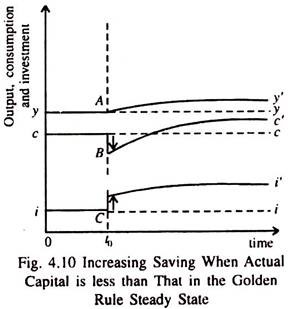
When an economy starts with less capital than in the Golden Rule steady state, public policy can be used to raise the saving rate to reach the Golden Rule. In Fig. 4.10 the increase in the saving rate in time t₀ leads to an immediate fall in consumption and a corresponding rise in investment.

With the passage of time as more and more investment occurs the economy’s capital stock continues to increase. With capital accumulation, output, consumption and investment continue to increase. The process comes to halt only when each variable reaches its steady state level.

Since the initial steady state was below the Golden Rule, an increase in saving ultimately leads to a higher level of consumption than what originally prevailed. However an in­crease in the saving rate can just enable an economy to move from one steady state to an­other.

This is known as the transitional dynamics of the Solow model. An increase in the saving rate cannot explain the sustained growth of Western countries since the 1950s.

Welfare Implications of Golden Rule Steady State:

The new steady state requires a sacrifice of consumption in the initial period. But, ultimately, the Golden Rule steady state raises consumption level arid, thus, the level of economic welfare. The opposite happens if the economy begins above the Golden Rule.

In such a situation the economy attains higher consumption at all points of time after reaching the Golden Rule. When the economy starts below the Golden Rule, it has to reduce consumption initially in order to increase consumption in the future if it is to reach the Golden Rule sooner or later. The contrast is significant.