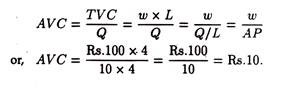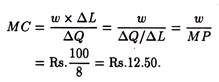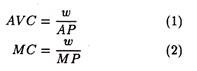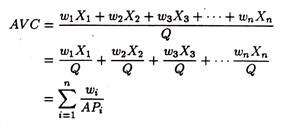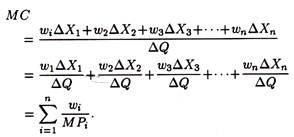Short-Run Costs and Production (With Diagram)

In this article we will discuss about the relation between Short-Run Costs and Production.

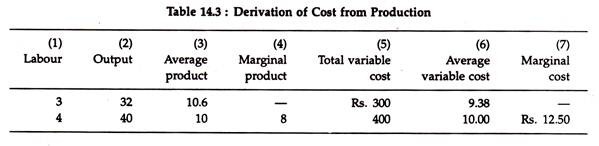
There is a close relation between production and cost in the short-run since one is a mirror image of the other. Since in the short run labour was considered to be the only variable factor, columns (1) and (2) of Ta­ble 14.3 show the points on the production function for three and four units of labour, which can pro­duce, respectively, 32 and 40 units of output.

The av­erage and marginal products are shown in columns (3) and (4). (Since we do not have total output for two workers, we cannot compute the marginal prod­uct of the third worker.)

Let us suppose that the wage rate is Rs. 100 per worker. Thus, if three workers are employed to pro­duce 32 units of output total variable cost will be Rs. 300, as shown in Column (5). Likewise, producing 40 units of output with four workers will cost Rs. 400.

Thus the average variable cost at an output of 40 units is TVC/Q = Rs. 400/40 = Rs. 10. If labour is the only variable factor total variable cost will be the product of the price per worker (Rs. 100) and the number of workers (four), and average variable cost may be expressed as:

There is a similar relation between marginal cost and marginal product. Since marginal cost has no relation to fixed cost and is treated as marginal vari­able cost, the extra cost of adding an additional worker to produce an additional 8 units of output is ∆TVC/∆Q = Rs. 100/8 = Rs. 12.50.

In the case of only one variable factor (labour), the marginal (vari­able) cost is the change in variable cost from produc­ing the additional 8 units of output and is obviously the cost of hiring the additional unit of labour, Rs. 100. Here the additional output of 8 units is nothing, but the extra contribution (marginal product) of the additional worker. Thus we can write marginal cost as

Thus, in the short run, when labour is the only variable factor, the following relations do hold:

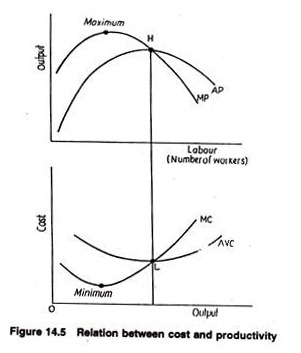
These relations enable us to determine the shapes of the average variable cost and marginal cost curves. So long as average product of labour increases, average variable cost will fall (assuming that the wage rate remains fixed at a particular point of time). When average product falls, AVC increases. Thus, when average product is maximum (constant) average cost is minimum (constant).

Therefore, since average product first increases, reaches a maximum, then diminishes, average vari­able cost first decreases, reaches its minimum (when average product is maximum), then increases. The shape of the average product curve generates a U- shaped AVC curve.

Thus ATC is U-shaped because AVC is U-shaped and AVC is U-shaped because of the Law of Variable Proportions. So we discover a close relation between the Law of Diminishing Re­turn and the shape of the short run average cost curve. The same type of relation can be discussed between the Law of Diminishing Return and the shape of the MC curve. It is to this relation that we turn now.

From equation (2) above, we observe that as marginal product rises, marginal cost falls; when marginal product falls, marginal cost rises. Marginal cost reaches its minimum point when marginal pro­duct attains its maximum. (See Fig. 14.5.)

The same analysis can be extended to cover a situation which employs several variable factors in the short-run. The average products of some inputs may be increasing while that of others are falling.

But with some inputs fixed, the decreasing average products will gradually outweigh those that are ris­ing, and average variable cost will start rising. Ul­timately, all average products must diminish since the usage of some inputs is fixed.

The same logic dictates that a similar situation holds for the relation between marginal product and marginal cost in the case of several variable factors. Eventually, declining marginal products will surely cause marginal cost to rise.

We may now generalize the relations in the case of several variable factors. Let us suppose that there are n variable factors. We may write the quantities of these inputs used as X₁ ,X₂, X₃, …. X_n and their respective prices as w₁, w₂, w₃, ….w_n. Thus

where AP_i is the average product of the i-th fac­tor. Again, the diminishing average products of the variable factors must, after a point, cause AVC to rise.

In a like manner, marginal cost can be expressed as:

As in the case of AVC, the diminishing marginal products of the variable factors must, after a certain stage of the production process, cause marginal cost to rise.

Irrelevance of Fixed Cost in Business Deci­sions:

Marginal cost is by far the most important cost concept used for marginal decision-making purpo­ses, and fixed costs have no decision significance. To verify this point let us consider a simple ex­ample. The manager of a restaurant which is open from 6.00 a.m. to 10.00 p.m. is thinking of keeping the restaurant open 24 hours a day.

Under the cur­rent 16-hour-per-day operation, the restaurant aver­ages Rs. 1,700 per day in revenues with total costs of Rs. 1,600 per day. Of this Rs. 240 per day is fixed cost-interest payments on bank loan.

The marketing manager carries out a survey and reaches the conclusion that keeping the restau­rant open the additional eight hours would increase average daily total revenue to Rs. 2,150 and average daily cost to Rs. 2,000. Thus, the marginal revenue from remaining open all night is expected to be Rs. 450; the expected marginal cost is Rs. 400.

Since the marginal revenue exceeds the marginal cost by Rs. 50 per day, on an average, the same amount would be added to profit. Hence, the restaurant has to be opened the additional eight hours.

Thus it is clear that, in making the decision, the manager considers only marginal cost. Fixed cost is not considered at all.

To verify this point let us sup­pose that the manager had allocated a proportion of fixed cost to the additional eight hours. If this were done, 1/3 of the fixed cost Rs. 80 would be added to the cost of keeping the restaurant open the ex­tra time.

Thus, the total cost of remaining open the additional time is found to be Rs. 400 + Rs. 80 = Rs. 480, which exceeds the additional revenues that would be generated. Therefore, the decision would be to keep the restaurant closed at night. But we have noted that staying open adds Rs. 50 a day to profit.

Thus, if fixed cost are taken into consid­eration an incorrect decision would be reached at. Marginal changes are all that matter when making such apparently unprofitable decisions. The point is, therefore, when making decisions about changes, only marginal cost should be consid­ered. Fixed cost is irrelevant.