Value of Money: Meaning, Measurement and Preparation of Index Numbers

“The yard measures distance”, said the teacher. “But what measures the yard?” was the question. “Well”, came the reply, “distance itself’.

Similarly money measures “goods”. But what measures money?

“Goods” is the reply. Value, as we know, is the ratio of exchange between two goods, and money measures that value through price. Money is an object of desire. Efforts are made to obtain it not for its own sake but for the goods it can purchase.

The value of money, then, is the quantity of goods in general that will be exchanged for one unit of money. The value of money is its purchasing power, i.e., the quantity of goods and services it can purchase. What money can buy depends on the level of prices. When the price level rises, a unit of money can purchase less goods than before. Money is then said to have depreciated. Conversely, a fall in prices signifies that a unit of money can buy more than before.

Money is then said to appreciate. The “general level of prices” and the value of money are thus the same thing from two opposite angles. When the prices rise the value of money falls and vice versa. In other words, the value of money and the general price level are inversely proportion­s’ to each other. Violent changes in the value of money (or the price level) disturb economic life and do great harm. We must, therefore, carefully study the factors which’ determine the value of money.

Suppose we have found by measurement that a room is four metres long. Measuring it again next day we are surprised to see that the same room is five metres in length. How could the room stretch itself by a metre overnight? Was some partition knocked out or an extension added during the night? Or is it that our metre measure has grown shorter by 2 centimeters? Which out of these is the correct answer? In the same way, if a rupee can buy one kg of wheat today but purchases only half a kg tomorrow, we are greatly perplexed.

We feel disgusted with our food-measure, the rupee, which has shrunk to half its length. We want to know what has happened. We are told “the value of money has changed.” Exactly this is what has happened in India. There are many times more rupee notes circulating in the country now than previously, while the number of goods has not increased to that extent. Hence a rupee buys less.

Measurement of Changes in the Value of Money:

Changes in prices are not uniform. Some prices rise, others fall; while still others remain stationary. They are like bees dashing out of a hive higgledy-higgledy, some buzzing off this way, some that way, while others keep hovering at the spot. But there may be a trend in a particular direction. A comparison of price changes would give a very confusing picture. We have to discover the extent of the overall changes in the value of money before suggesting a remedy. The seriousness of the disease must be known before a remedy can be suggested.

Index Numbers:

The device of index numbers comes to our aid in measuring changes in the value of money or price level. An index number is a statement in the form of a table which represents a change in the general price level. Index numbers have great importance in these days. When it is desired to find out to what extent prices have risen or fallen, an index number is prepared. In every advanced country, index numbers are being regularly prepared officially by the governments and also non-officially by other bodies interested in economic changes.

Preparation of Index Numbers:

The following steps are necessary for the preparation of index numbers:

(a) Selection of the Base Year:

The first thing necessary is to select a base year. It is the year with which we wish to compare the present prices, in order to see how much the prices have risen or fallen. The base year must be a normal year. It should not be a year of famine, or war, or a year of exceptional prosperity.

(b) Selection of Commodities:

The next step is to select the commodities to be included in the index number. The commodities will depend on the purpose for which the index number is prepared. Suppose we want to know how a particular class of people has been affected by a change in the general price level. In that case, we should include only those commodities which enter into the consumption of that class.

(c) Collection of Prices:

After commodities have been selected, their prices have to be ascertained. Retail prices are the best for the purpose, because it is at the retail prices that a commodity is actually consumed. But retail prices differ almost from shop to shop, and there is no proper record of them. Hence we have to take the wholesale prices of which there is a proper record.

(d) Finding Percentage Change:

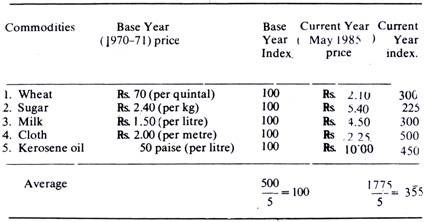
The next step is to represent the present prices as the percentages of the base year prices. The base year price is equated to 100, and then the current year’s price is represented accordingly. This will be clear from the index number given on the next page.

(e) Averaging.

Finally, we take the average of both the base year and the current year figures in order to find out the overall change. In May 1985, the price index was 355 which means that the price on the average were more than three-and a-half times as much or 255 per cent higher than what they were in 1970-71.

Uses of Index Numbers:

Index numbers can be used for a number of purposes:

(i) Index numbers are used not merely to measure changes in the price level or changes in the value of money. They can be used to measure quantitative change. Thus, we can prepare an index number of wages, imports, exports, industrial production, unemployment, profits, area under cultivation, enrolment in a college, etc.

(ii) Such quantitative changes as are measured by index numbers can indicate social and economic trends and help in framing policies with respect to them. For instance, an index number of cost of living can guide us in the adjustment of wages to changing prices.

(iii) We can also compare, with the help of index numbers, economic conditions of a class of people at two different periods.

(iv) Index numbers can be used as basis for, and equitable discharge of, contracts relating to borrowing and lending. We know when prices rise, creditors lose. It may perhaps be considered more just to ensure that the creditor gets back the same purchasing power. Hence, when prices rise, the debtor may be asked to pay a correspondingly higher sum to discharge a debt.

Limitations:

It may, however, be pointed out that index numbers are not a faultless guide.

They suffer from a number of limitations, some of which are given below:

(i) Approximations:

Index numbers are at best only approximations. They cannot be taken as infallible guides. Their data are open to question and they lead to different interpretations.

(ii) International Comparisons Difficult:

Use of index numbers for inter­national comparisons presents several difficulties. The result is that such comparisons are difficult, if not impossible, on account of the different bases, different sets of commodities or differences in their quality, etc.

(iii) Comparisons between Different Times Difficult:

It is not easy to institute comparisons between different periods of time. Over long periods, some popular commodities are replaced by others. Entirely new commodities come to figure in consumption, or a commodity may be vastly different from what’ it used to be. Think of a modern railway engine and one of the early ones. Ford cat 1985 is a different commodity from the 1950 Ford.

(iv) Measure Sectional Price Levels Only:

Index numbers measure only changes in the sectional price-levels. An index number, therefore, prepared for a particular purpose, may not be useful for another. An index number that helps us to study the economic conditions of mill-hands or railway coolies will be useless for a study of the conditions of college lecturers.

An entirely different set of commodities will have to be selected. Different people use different things and hold different assets. Therefore, different classes of people are affected differently by a given change in the price-level. Hence, the same index numbers cannot throw light on the effects of a price change on all sections of society.

(v) Weighting Changes Result:

One set of weights may yield quite a different result from another, and weighting is all arbitrary.

Conclusion:

We may conclude in the words of Coulborn who observes, “No general price-level is in fact compiled in this way because the practical difficulties of collecting the various prices and assessing weights strictly appropriate to the base year, and approximately relevant to the subsequent ones, prove to be difficulties which are insuperable in practice”