Price Index: Meaning, Uses and Importance

Let us make an in-depth study of the meaning, uses and importance of price index.

Meaning:

Changes in the levels of prices are mea­sured using a scale called a price index. This is the most useful device for measuring change in the price level.

In most countries price indexes are used to measure inflation, each focusing on the prices of a collection of goods and services important to a particular seg­ment of the economy.

The consumer price index focuses on goods and services typically purchased by households; the producer price index focuses on goods purchased by business; and a GDP chain-type index measures price changes in the economy as a whole. To able to the index numbers we most know what a price index is, how it is constructed, and how it is interpreted.

A price index is a measure of price changes using a percentage scale. A price index can be based on the prices of a single item or a selected group of items, called a market basket. For example, several hundred goods and services—such as rent, electricity, and automobiles—are used in calculating the con­sumer price index. Because a market basket includes a range of goods and services, it pro­vides a more comprehensive measure of inflationary pressure than a single item would.

Compilation and Uses of Price Indices:

We know that goods and services are valued in terms of money. Their prices indicate their relative value. When prices go up, the amount which can be bought with a fixed amount of money goes down; when prices fall, the amount which can be bought increases. In other words, when prices fall, the value of money rises; and when prices rise, the value of money falls.

An index number is a statistical device used to express price changes as a percentage of prices in a base year (or at a base date). (This base date is indicated by a phrase such as ‘1980= 100’.) In this case, movement in prices are expressed as percentage changes over the average level prevailing in 1980.

In India there are various price indices such as index of retail prices, index of wholesale prices, cost of living index of industrial wor­kers, export prices, and so on. A separate index number can be calculated to measure changes in each price level. However, the method of construction is the same in each case.

An index number is simply compiled by selecting a group of commodities, noting their prices in a given year (the base year) and putting the number 100 to the total. If the prices of the selected commodities rise by, for example, 3% during the next year, the index number at the end of the year is 103. A fall in price of 1% would be shown by an index number of 99.

Two related points may be noted in this context:

1. The value of money:

Firstly, commodity prices, wholesale and retail, not only differ but also may be moving in different directions at different rates at any one time. So, there is no such things as ‘the value of money’. We have to think of the value of money in particular uses or in different sectors of the economy.

2. Retail price movements:

Even within any specific sector, e.g., the retail sector, each commodity will have different prices in diffe­rent places and even in different shops in the same town. Moreover, different people buy different things and even when they buy the same things they buy them in different quan­tities.

Thus, it is not proper to treat a fall in the average retail value of money as ‘a rise in the cost of living’. In only means that the cost to a certain section of society living in its normal manner has risen. A family in a different section of society may have experienced a greater or lesser rise—or even a fall in its cost of living.

Three Steps:

Three steps are involved in compiling a retail price index. Firstly, one has to decide which section of the population is to be covered by the index. Thereafter, one has to find out how the families concerned spend their money. Finally, one has to choose a base year for the index.

1. Which section of the population?

This depends on the purchase for which the index is to be used. If it is going to be used for regulating old age pensions the basis of the calculations must be the pattern of expen­diture of old people. If the index is going to be used to assess the welfare and economic progress of the community as a whole, infor­mation has to be collected from a cross- section of people (i.e., all classes of people). It would be in the lightness of things to eliminate the very rich and the very poor because their patterns of expenditure differ so much from the rest of the society that they, if included, would unduly distort the average picture.

2. What is the average pattern of expen­diture of the selected group?

This is found out by taking a survey of the expenditure of the families in the group. A random sample of families must declare every detail of expen­diture in a random selection of weeks through­out the year. On the basis of this information an average pattern of expenditure is calculated.

3. What should be the base date (year)?

In determining the base date of index—which should be as mean to the period of the survey as possible — it is important to consider nor­mal year(s). Any exceptional year(s) —such as the year(s) of war or emergency or revolution — has (have) to be avoided. This is because certain factors affecting prices during wartime are unlikely to be repeated in future (peace time).

The Basic Equation:

The equation for calculating an index num­ber for a given year is

rupee outlay for a given year/rupee outlay for the base year x 100

= price index number for a given year.

For example, in year 4, Rs. 600 are needed to buy what Rs. 500 bought in the base year. Putting these numbers into the equation yields.

Rs. 600/Rs. 500 x 100 = 120.0.

To determine an annual percentage change in prices between two consecutive years, 1 and 2, in a price index, use the following equation:

year 2 index number – year 1 index number/year 1 index number x 100

= annual percentage change.

For example if P₁, = 105 and P₀ = 100 of then annual price charge will be:

105 – 100 / 100 x 100%

= 5%

Method of Calculation:

The method of calculation is illustrated in Table 19.1. We use imaginary figures and include only three commodities in the con­sumption basket for the sake of simplicity.

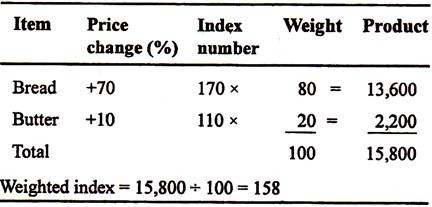
The method can be simply explained by assuming that the index covers only two items —say bread and butter. It would, of course, be easy to take a simple average of their price changes over any period, but this would not give a true indication of the change in their combined cost to consumers unless house­hold expenditure on each commodity happened to be the same.

For instance, if the price of bread rose by 70% and butter by 10% the average increase would be 40%. But their combined cost would not rise by exactly that average if consumers spend more on, say, bread than on butter.

To take account of the different significance of items in the index, a system of weights is adopted. In a retail price index each item is weighed according to its relative importance in the average family budget.

Thus, if out of every rupee spent each day on bread and butter 80P goes on bread and 20P on butter, the ratio of 80 to 20 reflects their relative importance and these figures represent their respective weights out of a total of 100. By using the weights, our index takes account of the fact that consumers spend four times as much on bread as on butter.

Let us now calculate the weighted index on the original assumption that the price of bread rose by 70% and butter by 10%. First, it is custo­mary to express percentage price changes in an index by calling all prices 100, on the starting (or base) date.

The percentage increases for bread and butter are thus represented by the numbers 170 and 110 respectively. (If a price fell by, say, 10%, the number would become 90.) The index number for each item is then multiplied by its weight. The resulting products are next added together and the total finally divided by the sum of the weights as illus­trated in Table 19.2.

Table 19.2: Index Number Calculation:

The weighted index figure of 158 shows a combined price increase of 58% instead of a 40% increase using an un-weighted average. The difference arises because the larger price increase was for bread on which our consumers spend more.

Importance of Indexes:

The consumer price index and other measures of inflation are not studied by academics, business people, and government officials out of idle curiosity. Rather, the indexes have an important impact on policymakers’ decisions and on the operation of the economy. They directly affect wages of union workers who receive cost-of-living adjustments based on the consumer price index, and they influence the size of many non-union income payments as well.

Employers and employees often look to these indexes in determining “fair” salary increases. Some government programmes, such as social security, base changes in monthly checks on a variation of one of these indexes. Private business contracts may provide for price adjustments based on the producer price index and, in some instances, other payments such as child support and rent have been tied to one of these indexes.

Index numbers can be used for a variety of purposes. By comparing the index numbers of several years in succession we can find out whether the price level is rising or falling and the degree of change. Appropriate measures can then be taken by the government to coun­teract the bad effects of price changes in either direction.

Cost of living index numbers can be used to judge the conditions of the working class. In some countries, wages are varied in proportion to the changes in the cost of learning index number so that the workers may not suffer distress when prices rise.

Index numbers are useful for comparing the price situation of one year with that of another. For example, the index numbers of the years 1939 to 1945 show how the price level and the value of money changed during these years. But long range comparisons should not be made. It is useless to compare the index number of 1939 with that of 1999.

The reason is that in 1999 many new commodities have come into existence and most of the commodities of 1939, which are still in use in 1999, have considerably changed in quality. When the time interval is much too long, there is no common base for comparison. This is also true for index numbers of different countries.