Here is a comparison between transactions and cash balance approaches.
It may be clearly understood that there is no doubt about the superiority of cash balances version over the transactions version of the quantity theory of money.
The difference between the two versions is not as fundamental as might appear at first sight.
A closer examination of the two approaches will show that they are more or less similar as both the versions show that the price level depends upon the quantity of money. Both the approaches can be easily compared.
ADVERTISEMENTS:
P = MV/T (Fisher) or M/KT (Roberson)
These equations make use of the same symbols implying more or less the same thing. The two equations show that V and K tend to be the opposite of each other. The higher the fraction of the real income that people hold in money, the lower will be the velocity of money and vice versa. V and K are reciprocals V = 1/Kor K = 1/V. It means that when people want to hold more (higher the K), the velocity of circulation of money will be less (lower the V). If, therefore, we want to enquire into the causes of the fluctuations in the velocity of money, we should turn to the causes which determine changes in the factor K.
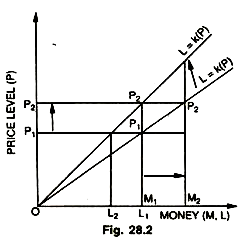
In fact, the two versions can be reconciled by substituting 1/V for K and 1/K for V in the two equations. The new term K, represents the ratio of cash balances desired relative to the national income, thus emphasizing the role of money as a store of value. The Cambridge cash- balances equation stresses the role of money as an asset, whereas the transactions approach stresses the use of money as a circulating medium. We can demonstrate the similarity between the two versions with the help of the Fig. 28.2.
In the figure as the quantity of money increases from M1 to M2, there is a direct effect on the price level which rises from P1 to P2. This is what quantity theory transactions approach tells us. But the mechanism through which cash balances approach operates is different. The equation L = k (P) shows that the demand for cash balances is related to price level. With changes in the demand for cash balances (L) there are proportionate and corresponding changes in price level (P). with a reduction in the demand for cash balances, from L1 to L2, price level (P) rises from P1 to P2. This is because the reduced demand for cash balances (L1, L2) releases the same amount of money for exchange, which raises prices.
ADVERTISEMENTS:
There are, however, some notable differences between the two versions. Firstly, the two approaches give different interpretations to the demand for money. In the transactions approach money goes round and has wings, it is needed to exchange goods and services. In the cash-balance approach money is flat and remains idle, it is used as a store of value. Secondly, the stress in the transactions theory is on the velocity of money (V), while in the cash-balance theory, the stress is on idle balances kept as a part of national income (K). Further, the cash-transactions equation gives attention to money as a flow, while the cash-balances equation gives attention to money as a stock. Moreover, Fisher’s equation explains the value of money over a period of time, while the Cambridge equation explains the value of money at a particular moment of time.
Pointing out the difference between Marshallian version of the cash balances, equation and Fisher’s equation of cash transactions equation, Prof. Hansen remarks, “The Marshallian version of the quantity theory, M = kY = represents a fundamentally new approach to the problem of money and prices. It is not true, as is often alleged, that the cash balances equation is merely the quantity theory in new algebraic dress……. To assert this is to miss entirely the significance of the k in the Marshallian equation………. The difference can be stated as—in terms of the Marshallian approach, sudden and rapid shifts in the desire of the public to hold money may profoundly affect prices even though the monetary authority successfully maintains a high stability in the money supply. The desire of the public to hold cash balance—liquidity preference—enters as a powerful factor. Drastic and sudden shifts in the desire to hold money, reflected in a change in k, may produce large and quickly moving changes in the level of income and prices. Shifts in public psychology in expectations, must be taken account of not less than changes in money supply. In the Marshallian analysis a shift in k may start an upward or downward movement. It is k, and not M, that holds the stage.”
Advocates of the Cambridge equation did not consider themselves to be in any fundamental disagreement with Fisher—their primary concern was the price level and for the most part they accepted the basic conclusions that the value of money varied inversely with its quantity. At the same time, they considered their approach superior to that of the transactions version. In their approach major attention was given to the role of the demand for money.
ADVERTISEMENTS:
It was this emphasis on the subjective nature of the demand for money which provided the psychological insight lacking in the transactions approach and which rendered the cash balance approach, in Pigou’s words, “A more effective engine of analysis.” Moreover, by specifying more precisely the constituents of the demand function, the Cambridge approach also indicated the conditions which would give rise to unstable fluctuations in demand.
The beauty of the Cambridge approach lay in spotlighting and explaining the change in k ; in contrast, the mechanical nature of the transactions approach provided no insight into why the value of V should ever change. Thus, while the Cambridge approach may be formally identical to Fisher, in one sense it went further in indicating possible psychological and institutional factors which were ignored in the quantity theory. In essence, this was all that divided Fisher and the Cambridge School.