The speculative demand for money was given by Keynes. According to Keynes: transaction demand for money (L1) is only one part of total demand (L) the other part being speculative demand for money (L2) ... L = L1 + L2
The ‘speculative motive’ for holding money arises because:
1. When interest rate changes, the capital value of money does not change, and
2. There is uncertainty about how the interest rate will change in the future.
ADVERTISEMENTS:
As far as the choice between holding bonds and money was concerned, Keynes viewed that it will depend on the expectations regarding the future interest rate. But, Tobin viewed that: individuals hold diversified portfolio of financial assets in form of money, securities, bonds etc.
Holding securities involve an element of risk, that is, of capital loss or capital gain on the security, thus, holding of bond is based on uncertainty, such uncertainty creates a real cost to the investor and thus influences the demand for money. Tobin with the help of Portfolio optimization approach tried to explain the speculative demand for money.
Portfolio approach is based on following Assumptions:
1. An individual has only money and bonds to choose from his asset portfolio.
ADVERTISEMENTS:
2. People treat wealth as good, therefore, prefer more wealth to less wealth.
3. People treat risk as bad, therefore prefer less risk to more risk.
4. His preference between risk and return is shown by the indifference curves which are known to him.
5. IC curve slopes upwards towards the right because people treat wealth as a good but. risk as a bad. There is a trade off between risk and return.
ADVERTISEMENTS:
Tobin viewed that if an investor holds more of bonds, it will carry both more income and more risk. This is because when interest rate decrease, bond price will increase. Investor will get a capital gain and vice versa. There is, therefore, risk associated with return on bonds measured by standard deviation (σ).
Greater the proportion of bonds held in asset portfolio, greater will be the risk but at the same time return will be greater. However, while choosing between money and bonds, he desires to earn income but dislikes risk. The investor will, therefore, need more income to compensate for the risk.
As diversified investor considers risk and return as imperfect substitutes, therefore, he is willing to take greater risk provided additional return increases. Therefore. IC are convex to X-axis. The investor has an indifference (IC) map and a budget constraint.
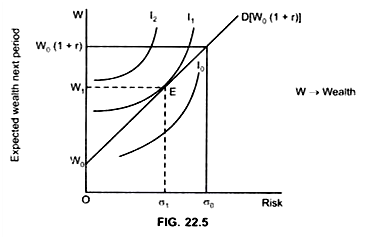
The Budget constraints represented by OD shows the combination of risk and expected wealth that an individual will choose while arranging his portfolio. Therefore, budget line is also called risk return line as it shows trade off between risk and return.
The OD curve is a straight-line starting from W0.
1. At W0 the entire portfolio is held in money, there no income and no risk. But this is an extreme situation.
Assume, expected value of gains and losses is zero (0).
Then, expected value of yield of holding bonds is equal to the market interest rate.
2. At point D, that is [W0 (1 + r)], the portfolio is held entirely in bonds and both income and risk are maximum.
ADVERTISEMENTS:
If all bonds offer the same interest rate and carry same risk, then the wealth holder can choose any combination of wealth and risk (money and bonds) along the OD line. Greater the bonds the investor holds, greater is the expected return and greater is the risk.
Objective of the wealth holder:
At a given interest rate and risk attached to holding bonds, the investor will try to get maximum utility from his portfolio, i.e., he would hold a combination of money and bond so as to get maximum utility.
This will be achieved where:
ADVERTISEMENTS:
The highest possible IC (I1) is tangent to the Budget line, that is, where the slope of IC = slope of Budget line.
This is at point E on I1 (Fig. 22.5)
I1 is tangent to the budget line at point E
ADVERTISEMENTS:
... At point E: Slope of IC = Slope of Budget line
Expected return from investment in bonds = W1
Risk involved = σ
If, investor prefer to hold all his wealth in form of bonds then his expected wealth will be W0 (1 + r)
Where r → interest rate.
σ0 → maximum risk associated with investment in bonds