Impact of Monetary and Fiscal Policies in the IS-LM Model (With Diagram)

Let us make an in-depth study of the Impact of Monetary and Fiscal Policies in the IS-LM Model.

It may be noted that the impact of monetary and fiscal policies in the IS-LM model depends also on interest elasticity of the transaction demand for money.

If transactions demand for money becomes sensitive to interest rate changes, as has been postulated by W. J. Baumol and James Tobin, monetary policy loses its effectiveness and fiscal policy becomes more powerful as a stabilisation weapon.

This proposition may now be proved.

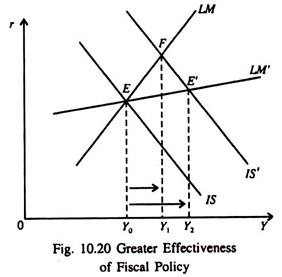
So the denominator of equation (2) increases or the slope of the LM curve falls. So fiscal policy becomes more effective and monetary policy becomes less powerful. See Fig. 10.20 and Fig. 10.21.

In Fig. 10.20 as the LM curve becomes flatter due to interest elasticity of the transactions demand for money, a shift of the IS curve to the right increases Y from Y₀ to Y₂ which is greater than the increase from Y₀ to Y₁ when the LM curve is less flat, i.e., when interest elasticity of transactions demand for money is zero.

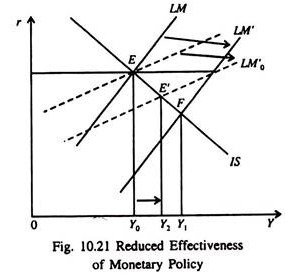
In Fig. 10.21 income increases from Y₀ to Y₁, due to monetary expansion if the transactions demand for money is not interest elastic as shown by points E and F. If, however, the transactions demand for money becomes interest elastic and the LM curve shifts from LM₀ to LM’₀, the economy reaches equilibrium at point E’.

This means that income rises from Y₀ to Y₂ which is less than the increase in income from Y₀ to Y₁, in the situation where transactions demand for money does not depend on the rate of interest. Thus monetary policy loses its effectiveness to some extent if transactions demand for money is sensitive to changes in the interest rate.

i. Interest Elasticity of Money Supply and the Effectiveness of Monetary Policy:

When the LM curve is vertical (the classical case) fiscal policy has no multiplier effect on the level of Y. This prediction is true because we assume that the money supply remains constant. It is quite possible for the central bank to manipulate the money supply so as to keep r constant.

In this case we can speak of money supply function M =f(r), which is fairly elastic with respect to r. It is quite obvious that the central bank will increase the money supply whenever there are signs of an increase in r, and reduce M when r shows signs of falling. If M is highly elastic with respect to r, the LM curve becomes flat (as in the liquidity trap case) and fiscal policy has larger impact on the level of output or income (Y).

Monetary and Fiscal Policies and the Composition of Output:

Both monetary and fiscal policy can be used to expand demand and raise the equilibrium level of output. Except in two extreme situations — the liquidity trap case (the horizontal LM curve) and the classical case (the vertical LM curve) monetary and fiscal policies can be used to affect the level of output.

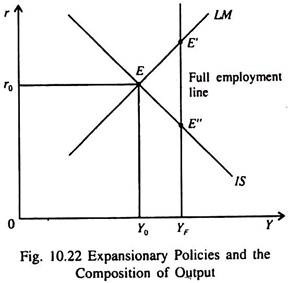
In Fig. 10.22 we show the effect of changes in macroeconomic policy not on the level of output as such but on its composition. Here the economy is initially in equilibrium at point E with an output level of Y₀, below the full employment level Y_F.

An expansionary monetary policy could be an ideal choice in such a sub-optimal situation. By increasing the money supply it is possible to shift the LM curve to the right, reduce r and raise aggregate demand and enable the economy to reach point E”. Alternatively by using an expansion­ary fiscal policy it is possible to shift the IS curve to the right and enable the economy to reach point E’.

Finally a combination of the two policies can be used to an enable the economy to reach the point of full employment.

What is important here is that the choice of a policy may be made on the basis of the desire of the government to alter the composition of output, without changing its total.

An expansionary monetary policy can be used to stimulate the interest-elastic component of aggregate demand (mainly investment spending and, in particular, residential construc­tion). In truth, monetary policy has the immediate and the strongest effect on residential construction.

In contrast, the effect of fiscal policy depends on exactly what goods the government buys or what changes it incorporates in the tax-transfer programmes.

Each policy affects the level of aggregate demand, but the composition of output will differ from case to case. A cut in corporate tax rates affects both investment spending, and, through distributed profits (and thus personal disposable income), personal consumption.

A personal income tax cut has a direct effect on consumption spending. Given the quantity of money, all expansion­ary fiscal policies raise the interest rate (by increasing Y and thus the transactions demand for money).