Get the answer of: What are the Possible Shapes of the Consumption Function?
Technical attributes or what we call the properties of consumption function imply an understanding of the shape, position and slope of the consumption function.
There are many conceivable shapes that the consumption function could take.
But two shapes are commonly discussed. One is that it is a straight line rising from left upwards to the right. The second shape is that of a curve. The former is called a linear consumption function while the latter is called a curved consumption function.
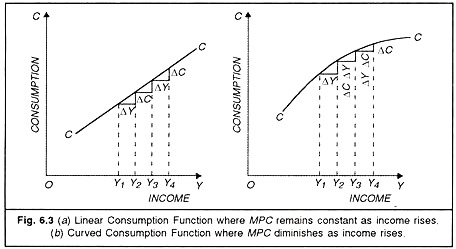
When we ask the question as to what is the nature of relationship between income and consumption—we, in other words, simply ask about the shape and position of the consumption function. We depict the two possible shapes and positions of the consumption function in the following diagrams. Figure 6.3(a) shows a linear consumption function.
It is a straight line. Y1Y2, Y2Y3, are equal successive increments in income as measured by ∆Y’s. We find that the resulting increments in consumption, ‘∆C’s, are also equal. But they are all less than ‘∆Y’s. In other words, the ratio ∆C/∆Y remains constant whatever the level of income, that is, MPC remains constant in a linear consumption function. A straight line has a constant slope throughout.
While statistical studies of consumption behaviour have tended to support a linear consumption function in macroeconomic theory, a curved consumption function is not ruled out. Figure 6.3 (b) shows a curved consumption function. Let us find out the implications of such a consumption function.
It should be readily clear from the diagram that while ‘∆F’s are equal, ‘∆C’s go on diminishing with successive equal increments in income. It means that with equal increments in income, increments in consumption diminish. ∆C/∆F continues to decrease in a curved consumption function. This means that MPC continues to diminish in a curved consumption function.
ADVERTISEMENTS:
The consumption function curve goes on flattening out to the right. Since MPC can never fall to zero or be less than zero, the curve of consumption function can never fall downwards: at the most it can be flat, parallel to the horizontal axis.
In the many field surveys on household behaviour, however, marginal propensity to consume is found to be constant for all income levels. The information obtained is such that it will justify a straight line (linear) consumption function. MPC calculated from statistical data collected in U.S.A. is found to be almost constant, i.e., between 0.6 and 0.8 in most cases. In most of these studies it was the long-period consumption function which was considered.
There are two versions explaining the linear shape of the long-period consumption function:
(1) The life-cycle hypothesis, and
ADVERTISEMENTS:
(2) The permanent income hypothesis.
According to the first approach, families, consciously or subconsciously, estimate their long-range incomes over the years ahead and adjust their consumption expenditures and saving to these rough expectations. Generally, people adjust their expenditure in such a way that at various stages, as their incomes increase, consumption increases at the same rate. Thus, for typical families (classified income-group-wise), average ratio of consumption to income is similar and stable at all income levels. In the same way, consumption is a stable function of income for the population as a whole.
The second approach, popularly called permanent income hypothesis is closely related. Milton Friedman, the main proponent of the view, argues that families base their consumption on what they expect their “permanent income to be”. Temporary variations in income up or down this permanent expectation of income will generally not affect consumption spending greatly.
Rather, if income falls temporarily the families will cut their savings, use up their liquid assets, or go into debt to maintain consumption. If there is a temporary increase in income, it is likely to go mainly into saving (including consumer durables). Both these approaches are supported by empirical research findings in the United States.
Whether consumption function is linear or curved this in no way affects Keynes’ basic theory. The validity of the theory certainly does not depend upon the assumption of falling MPC. If the consumption function is linear, it merely reflects that the MPC would be the same at all points.
The only assumption basic to Keynes’ theory is that the absolute amount of consumption increases by less than the absolute amount of income whenever income increases. This may be expressed by saying that the slope of the curve must be positive and less than one which merely means that the marginal propensity to consume must be positive and less than one. Whether this is a correct representation of consumers’ behaviour, however, is a question of a fact on which further evidence must be sought.