Social Welfare Function of Economics (With Diagram)

In this article we will discuss about the social welfare function of economics, explained with the help of a suitable diagram.

The compensation principle only wants to know whether the losers could be compensated; it does not tell us that the losers should actually be compensated. It is argued that whether compensation should be provided and in what manner—all these are moral issues.

Another problem with the compensation criteria is that they only compare between a few alternatives to tell us what is the most desirable of these alternatives, but they do- not tell us the state that achieves the maximum possible welfare. Some economists thought, it was first suggested by Abram Bergson in 1938, that the problems with the compensation criteria could be solved by considering a social welfare function.

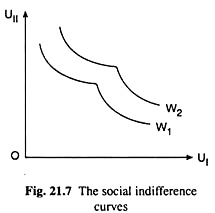
The social welfare function (SWF) is a sort of social indifference map consisting of the social indifference curves (SICs). An SIC gives the various combinations of utilities of the two individuals that comprise the society, that result in the same level of social welfare (W). To show this diagrammatically, let us denote the utilities of the two consumers by U_I and U_II.

The SWF then is:

W = f(U_I, U_II).

The SICs have been shown in Fig. 21.7. Each of them shows the different combinations of U_I and U_II that give a particular level of social welfare (W). SICs are negatively sloped because as I is made better off, II must be made worse off, to give us the same W.

If, at the initial (U_I, U_II) combination, both the individuals, or any one of them, are made better off, the utility level of the other remaining the same, then that would result in a higher level of W and the society would move to a higher SIC. In Fig. 21.7, W₂ represents a higher level of social welfare than W₁.

Let us note that the SICs need not be convex or concave to the origin. For there is no rule here that as U_I increases U_II would fall at a diminishing or at an increasing rate. Once we formulate the SWF and the SICs, we are well equipped to compare different policies and find out the policies that maximise social welfare subject to the available economic resources.

But how are we to obtain, or who is to determine, the combinations of U_I and U_II that would give the society the same level of welfare, or, who is to determine the combinations that would not give the same—but a lower or higher—level of social welfare? In a dictatorship, the dictator performs this function. Here the SWF and SICs reflect the value judgements of the dictator.

In a democracy, the value judgements must be determined collectively by the members of the society. The individuals can express their value judgements by means of voting. But Arrow pointed out that social welfare could not be evaluated by a democratic vote. This is known as Arrow’s Impossibility Theorem.

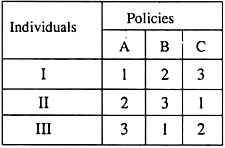
According to Arrow, the social welfare choices should be transitive, i.e., if situation A is preferred to situation B and B is preferred to C, then A is preferred to C. Given the transitivity assumption, let us now consider the following rankings of three policies A, B and C by three individuals I, II and III (the lower number indicating a higher rank).

From the above rankings we obtain: Individuals I and II prefer the policy A to policy B. Thus, a majority vote between the policies A and B will lead to the choice of A. Again I and III prefer B to C. So a majority vote between B and C will lead to the choice of B. Thus, we obtain A is preferred to B and B is preferred C. This would imply, because of transitivity, that A is preferred to C.

Therefore, if transitivity holds, we obtain A is preferred to B and A is preferred to C. Therefore, democratic vote gives us that A is the policy that should be selected. However, when we consider A and C, we find that both II and III prefer C to A.

So, the majority vote between A and C will lead to a choice of C, and transitivity will not hold. Thus, democratic votes lead to the choice of all the three policies, i.e., here we arrive at what is known as the voting paradox.

The above method of voting by ranks is paradoxical and confusing, and we may come out of it, if account is taken of the intensity of the preferences of different individuals, and a scheme of compensation is made use of. This is actually the idea behind the compensation principle.

For example, if the consumer I and II’s preference for A is very intense and it is worth, say, Rs 1000 to each, and consumer I and Ill’s preference for B, and II and Ill’s preference for C, are not so intense, it is worth Rs 100, say, for each of them, then certainly a compensation scheme might be worked out and policy A might be implemented.

However, the criterion of SWF and also the Kaldor-Hicks compensation criterion based on potential and not actual compensation, requires an assumption of omniscience on the part of the individuals evaluating the different policies.

But such an assumption is totally unrealistic, because individual’s utilities are highly subjective, and it is very difficult for others to evaluate them. Only actual compensation will help an evaluation. In many instances, however, it is not clear to whom compensation is to be made.