Let us make an in-depth study of the profit-maximising output decision for any firm.
Let us begin our analysis by looking at the profit-maximising output decision for any firm whether it operates in a competitive environment or not. Since profit is the difference between total revenue (TR) and total cost (TC), to find the firm’s profit-maximising output level, we must analyse its revenue and cost.
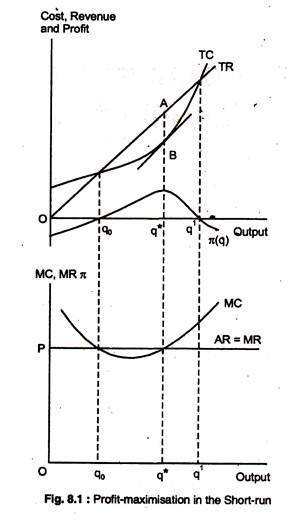
Suppose that the firm’s output is q, and that it gets revenue TR = p x q. The TC of production also depends on output. The firm’s profit is the difference between TR and TC. π(q) = TR(q) – TC(q).
To maximise profit, the firm selects the output for which the difference between TR and TC is the greatest. Fig. 8.1 shows TR is a straight line, since for a given price, P, TR increases proportionally with output, q. Its slope is the marginal revenue, MR. Because there are fixed and variable costs, TC is not a straight line; its slope is marginal cost, MC. TC is positive when output is zero because there are fixed costs in the short-run.
For smaller output than q0, profit is negative — revenue is not sufficient enough to cover cost (FC + VC). Here MR < MC, which means that increases in output will increase profit.
As output increases beyond q0, profit becomes positive and goes on increasing until output reaches q* where MR = MC and q* is the profit-maximising output where the vertical distance between TR and TC, AB, is greatest at this point; thus, π(q) reaches its peak. Beyond q* MR < MC, and profit falls as output increases.
To see why q* maximises profit another way, suppose output is less than q* and the firm increases output by one unit, it will generate more revenue than costs. In other words, MR > MC. Similarly, when output is greater than q*.
MR < MC. Only when MR = MC can profit be maximised. The rule is that profit is maximised when MR = MC, holds for all firms, whether competitive or not. This rule can be derived algebraically. Profit, π=TR- TC, is maximised where increment of output leaves profit unchanged.
ADVERTISEMENTS:
Δπ/Δq = ΔTR/Δq – ΔTC/Δq = 0. ΔR/Δq = MR, and ΔC/Δq = MC. Thus, we conclude that profit is maximised when MR(q) = MC(q).