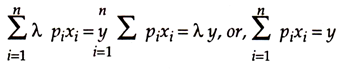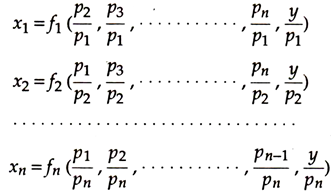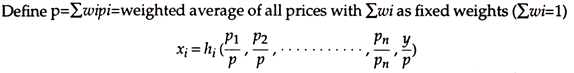Suppose all prices and the consumer’s income change in the same direction and in the same proportion. What will be the effect of such a change on the equilibrium purchase plan of a consumer?
The objective of the consumer is to maximise utility (u) subject to the budget constraint:
Expenditure aggregated over all goods = income
or, pixi = y.
ADVERTISEMENTS:
For a given set of prices (p1, p2,…………… , pn) this implies
There are n-1 such independent marginal utility ratios (if there are n different commodities). Marginal utility, like total utility, depends on the quantity of a good consumed. Therefore, the left hand ratios depend on the quantities of good consumed.
The marginal utility equations provide n-1 relationship between quantities and relative prices or price ratios. Together with the budget equation, we have n equations with which we can solve for each of the quantities as a function of all the prices and income.
ADVERTISEMENTS:
These demand functions have an important property: they are homogeneous of degree zero in prices and income. The implication is clear: if we raise all the prices and income of the consumer and raise them strictly in proportion, demand for no commodity will be affected as a result.
So, if all the prices in the marginal utility equations are multiplied by the proportionality factor, y, the equations are unaffected since this factor cancels in the numerator and the denominator of the price ratios.
Similarly, in the budget equation, this multiplying factor cancels from left and right sides as follows:
Thus, we write the theoretical demand functions as:
It is clear that the quantity demanded depends on all relative prices of the system and on real income.
This property of homogeneity could be expressed in another way.
In this form, the variable y/p is a more conventional measure of real income since it is, in effect, a ‘deflation’ of money income y by a weighted average of all prices of consumer goods.
A Numerical Example:
A simple example will rectify the property of homogeneity of the demand function. Suppose the income of a consumer is Rs. 100 and he is purchasing two goods—apple and orange. If the price of apple is Rs.2 and the price of orange is Re.1 per unit, respectively, he can buy 20 units of apple and 60 units of orange with his fixed income. Now, suppose, his income increases by 50% as also the prices of both the commodities.
So, in the new situation his real income or purchasing power will remain unchanged and he can buy the same old combination of the two commodities as before the price fall. (With Rs.150 he can buy 20 units of apple at Rs. 3 per unit and 60 units of orange at Rs.1.50 per unit.)