Derivation of Long Run Vertical as Curve (LRAS)

Derivation of Long Run Vertical as Curve (LRAS) to find the Relationship between Inflation and Output Level!

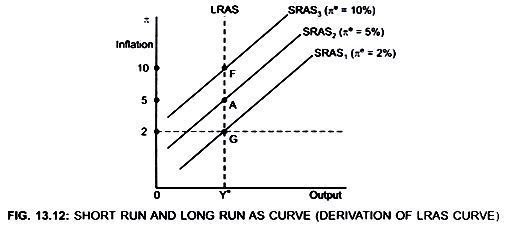
LRAS curve shows the relationship between inflation and output when actual inflation (π) and expected inflation (π^e) are equal, that is, π = π^e.

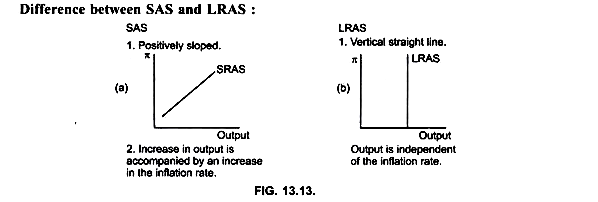
It shows that in the long run there is no trade off between inflation rate and output level because in the long run: Actual inflation = expected inflation.

LRAS is a vertical line at output Y^* obtained by joining points on SRAS curves at which π = π^e (Fig. 13.12) and there is no trade off between the two variables.

In short run:

With given π^e, higher inflation rates are accompanied by higher output.

Expectations Augmented AS curve:

In long run:

When the economy is at full employment level, that is Y = Y^*

Then π^e = π (expected inflation = actual inflation).

Thus LRAS shows that in the long run the level of output will be independent of the inflation rate. (Y = Y^*)

How are Assumptions made about expectations or

(i) Why is π^e included in AS function? or

(ii) What determines π^e? or

(iii) Why does SRAS curve shift? or

(iv) Why should the wage adjustment to inflation respond to yesterday’s actual inflation or tomorrow’s expected inflation? or

(v) How are expectations formed about π^e? or

(vi) What are the different ways of inflation adjustment compensation?

There are two formulations about π^e :

I. Adaptive Expectations Approach:

Expectations are adaptive if they are based on the past behaviour of inflation.

Under adaptive expectations, people expect inflation rate to rise at the same rate as it rose last year.

Therefore, under adaptive expectation, expected inflation rate (π^e) is equal to lagged inflation rate (π_t), that is:

There is no difference between last year inflation and expected inflation.

Limitation:

If expectations are adaptive it becomes impossible to tell whether the expected inflation (π^e) term in the AS curve represents π^e or compensation for past inflation.

If π^e = π_t, there is no difference between past inflation and expected inflation.

II. Another alternative is Rational Expectation Approach:

The approach was given by Robert Lucas and Thomas Sargen.

According to Mankiw:

“The rational expectations hypothesis implies that people do mistakes but they do not make systematic mistakes (like under-predicting inflation) in forming their expectations, These mistakes are easily spotted. People correct such mistakes and change the way they form expectations.” This model assumes that people base their expectations of inflation on all the information available about the future behaviour of inflation.

However, there cannot be any formula for expected inflation based on rational expectations. But still, Robert Lucas tried and was able to solve the macroeconomic problems of why are people not able to adjust their expectations quickly (a big hole in the expectations-augmented Phillips curve) to match the prediction by allowing for the role of mistakes.

Lucas is of the view that a good economic model should not rely on the public who makes easily avoidable mistakes.