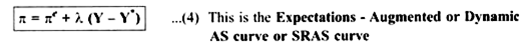Derivation of Expectation – Augment Philips Curve Equation from the AS Equation

Read this article to learn about Derivation of Expectation – Augment Philips Curve Equation from the AS Equation!

SRAS is derived from the Phillips curve. SRAS curve shows the relationship between output and the price level.

Milton Friedman and Edmund Phelps pointed out that the original Wage-Phillips curve equation (1) ignored the effect of expected inflation on wage rate.

Workers are interested in real wages and not in the nominal wage they receive, so they want that their nominal wage should include the expected inflation that would take place between the time the wages are fixed and the time when wages are paid which should be fully adjusted for the inflation they expect.

Firms agree to pay higher nominal wage because they will be able to sell their goods at a higher price. But when both wage and price rise at the same rate, both the workers and firms will be in the same position as they would be in the absence of inflation.

Hence, Friedman – Phelps theory suggested that inflation adjustment in wages compensates for expected inflation. Inflation adjustment will be a part of wage increase. Let π^e be expected inflation, then the growth rate of money wage Equation (3) can be written in form of:

Equation (4) shows that

π is determined by both:

(a) π^e and

(b) Unemployment or output.

Thus, dynamic AS curve incorporates expected inflation into the Phillips curve. The original Phillips curve did not take into account the expected inflation. It simply gave an inverse relationship between wage inflation and unemployment.

Properties of SRAS:

1. Dynamic SRAS shows positive relationship between inflation rate and level of output when π^e is held constant. Therefore SRAS curve is positively sloped. Given π^e, SRAS curve shows that inflation rate rises with the level of output. Higher the level of output, higher is the rate of inflation, This is because increase in output means an increase in demand for labour which in turn leads to an increase in wage and thus in price.

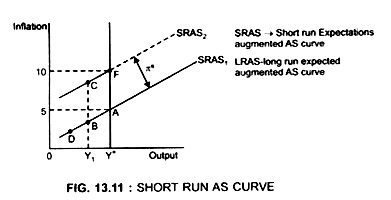
2. Expected rate of inflation affects the position of expectations augmented supply curve. Higher the π^e, higher is the SRAS curve (Fig. 13.11). For any π^e there’ll be a corresponding SRAS curve. Thus when π^e changes, the economy shifts from one SRAS to other. The distance between the two SRAS curves will be equal to the difference between the two expected rates of inflation. This implies that SRAS curves are parallel to each other.

π^e is constant on each SRAS curve.

π^e is 5% on SRAS₁. If expected inflation increases to 10%, SRAS curve shifts upwards from SRAS₁ to SRAS₂

Thus, π^e is 10% on SRAS₂.

3. SRAS curve shows that when the economy is at full employment level (Y = Y^*), then actual inflation (π) = expected inflation (π^e) e.g.

On SRAS₁ equilibrium at full employment output (Y^*) is at point A Where Y = Y^*, and π = π^e.

Similarly on SRAS₂ equilibrium is at full employment output level at point F

At all other points π ≠ π^e

e.g. when output is Y₁

π is less than 5% shown by point B on SRAS₁

But π is higher than 5% shown by point C on SRAS₂

Changes in π^e explain why Phillips curve breaks down.

4. SRAS is a flat curve which shows:

In the short run, very large change in output is required to generate a given change in inflation.

5. On each SRAS curve there is a tradeoff between π and output

To reduce π → reduce output → lead to recession → wage rate will fall due to unemployment → thus n rate will fall.

Conclusion:

SRAS curve shows that to decrease the inflation rate, output level has to be reduced because decrease in output (O) will lead to decrease in unemployment (U).

(O ↓ → ↓ U → ↓ W → ↓ π)

SRAS curve shifts up with π^e. The inflation rate, therefore, corresponding to any given level of output changes over the time as π^e changes.

Higher the π^e, higher is the inflation rate corresponding to a given level of output.

(Compare points B and C at output level → Y₁)

SRAS curve may also shift upward if supply shocks take place.