Interest Rate Parity and Financial Markets | Financial Markets | Economics

Interest rate parity is the result of arbitrage in financial markets. If US bonds and UK bonds are similar in every respect the currency used to pay the principal and interest, then they should yield similar returns to bondholders.

If US investors can earn a higher return from UK bonds, they are going to buy more UK bonds and fewer US bonds. This tends to raise the price of U.K bonds, pushing UK interest rates down. At the same time the price of US bonds drops, raising US interest rates.

The initial higher return on UK bonds and resulting greater demand for UK bonds increases the demand for pounds and increases the value of the pound in terms of dollar today. As the pound appreciates today, if investors expect the same future exchange rate as they did before the current appreciation, the expected appreciation over the future falls.

The change in the exchange rate and interest rates equalises the expected dollar return from holding a US bond and a UK bond. UK bonds originally offered a higher return than U.S bonds, but the increase in the demand for UK bonds relative to US bonds raises UK interest rates and the expected appreciation of the pound, so that bond returns are equalised. This explains why the interest parity condition must hold if the foreign exchange market is to be is equilibrium.

1. The domestic currency interest on the bond equals the foreign interest rate plus the per­centage change in the exchange rate.

2. Interest rate parity exists when similar financial assets have the same interest rate when measured in the same currency; or when the domestic interest rate equals the foreign interest rate plus the expected change in the exchange rate.

Equilibrium in the Foreign Exchange Market:

When the interest parity condition holds, i.e., when all expected returns are equal, there is neither excess supply of same type of deposit nor excess demand for another. Therefore, the foreign exchange market is in equilibrium when the interest parity condition holds. When dollar deposits offer a higher return than pound deposits, the dollar will appreciate against the pound as all investors try to shift their funds into dollar. The converse is also true.

The dollar should depreciate against the pound if pound deposits initially offer the higher return. Thus the interest rate parity condition explains how exchange rate changes help to maintain equilibrium in the foreign exchange market.

Covered Interest Arbitrage Parity:

If the financial markets are efficient then in equilibrium the risk-averse investor will be indiffer­ent between hedging the short-term foreign investment and hedging by using the forward market. Likewise, the risk-average short-term investor should be indifferent between the domestic and the foreign investments. The link among the spot market, forward market and the financial mar­ket that generates these equality conditions is established through covered interest arbitrage.

Let us consider an investor who has to decide whether to place funds at home (e.g., New York) or overseas (e.g., London). If he chooses to protect himself against the risk of spot rate fluctuations, that to do cover he will use the forward market. In this case the equilibrium con­dition is

i_NY – i_L = P … (1)

In equilibrium, any difference in the interest rates between the two financial centres has to be offset by the foreign exchange premium. This is the covered interest arbitrage condition. For example, if i_NY= 2.5% and i_L = 2% per quarter (i.e., 90 days) the financial and foreign exchange markets will be in equilibrium if the forward pound is contracted at a price which is 0.5% above the spot rate. In this case the investor in London is receiving 2% on the short-term investment plus 0.5% return due to the forward premium.

The sum of the two returns is equal to 2.5%, i.e., the return that an investor would receive on a short-term investment in New York. Thus it is clear that the interest rate parity condition cannot be maintained between the USA and the UK so long as forward rates differ from spot rates (even if markets are functioning efficiently, i.e. traders get all types of information and on time and there is no speculation).

Now if we take into account both the interest rates in the two countries and foreign ex­change markets we can easily predict the movement of financial investment between the USA and the UK.

There points are to be noted in this context:

1. If the interest rate differential (i_home – i_foreign) exceeds the forward premium (from the home country — here the USA — perspective) there will be an inflow of funds into the home country.

2. If the interest rate differential is less than the forward premium, there would be outflow of investment funds from the home country.

3. When i_home = i_foreign and P = 0 there will be equilibrium in the foreign exchange market and between short-term inflow of funds into or outflow of funds from the home country (the USA).

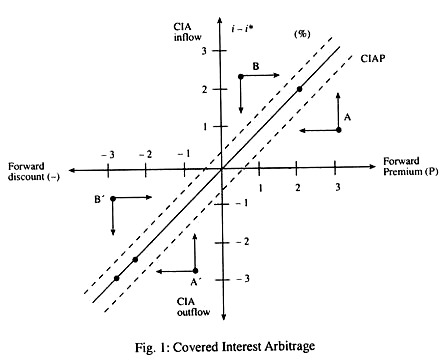
The interest rate differential between New York and London is shown on the vertical axis and the forward premium on the pound on the horizontal axis, with the minus sign indicating a forward discount and positive sign indicating a forward premium on the foreign currency in per cent per annum.

With the two axes scaled in the same way, the point of equilibrium between the interest rate differential and the premium are on the line that passes through the origin. This line is known as the covered interest arbitrage parity (CIAP) line.

The points above the line show disequilib­rium that will induce inflow of foreign investment into New York, while those points lying below the line also indicate disequilibrium which induces flow of funds from New York to London.

Above the CIAP line, either the interest differential exceeds the forward premium on the foreign currency or the negative interest differential is smaller than the forward discount on the foreign currency (point B’). In either case, it pays for foreigners (Britishers) to invest in home country (the USA) and there will be an arbitrage inflow. However, as the arbitrage inflow continues, the net gain diminishes and then disappears when the CIAP line is reached.

Starting from point A’, the transfer of funds abroad will increase the positive interest differ­ential (say, from 1 to 1.5) and reduce the forward premium (say, from +2 to +1.5) so as to reach the CIAP line once again. As funds move abroad (from the USA to the UK), interest rates tend to rise in the USA and decline in the UK. Since interest rates were already higher in the USA, the positive interest differential increases.

On the other hand, as American investors purchase the foreign currency (pounds) to invest in the UK, the spot rate rises. As Americans sell the foreign currency forward to cover their foreign exchange risk, the forward rate declines.

Thus the forward premium (i.e., the excess of the forward rate over the spot rate) diminishes. With the positive interest differential increasing and the forward premium decreasing, the net gain from arbitrage outflow diminishes. The process continues until A becomes zero when the CIAP line is reached and the arbitrage outflow stops.

Transaction Costs:

However, financial transactions are not costless. The interest rate dif­ference and the forward premium can differ in equilibrium by the amount of the transaction costs. When such costs are positive, CAIP does not exist. So the equilibrium condition of the financial market is:

i_Ny – i_L = P ± transaction costs

In Fig. 1, two dashed lines, drawn equidistant an either side of the CIAP line (at a rate of say 0.25%), indicate transaction costs. Financial and foreign exchange market equilibria will thus be in the neighbourhood of the CIAP line. The distance of such equilibrium from the CIAP line reflects average transaction costs.

Thus, in reality, interest arbitrage (inflow and outflow) will come to an end when the net gain reaches about 0.25% per year (or 1/4 of 0.25% per quarter). This range is shown by the area below the two diagonal dashed lines.