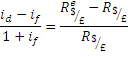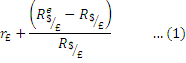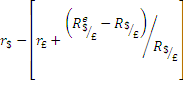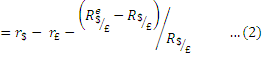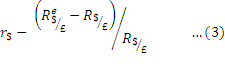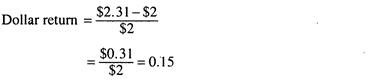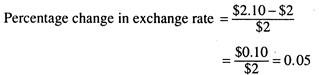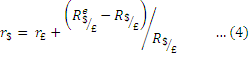Asset Approach to Exchange Rate | Foreign Exchange | Economics

Exchange rates are used to compare international prices of goods and services. They are also used to compare the return on foreign currency-denominated stocks and bonds to the return on domestic assets. In the 1970s, the stress was on the monetary approach to balance of payments.

The focus of attention in this approach was on international trade flows as primary determinants of exchange. One reason for this was that up to 1960s, government’s maintained tight restrictions on international flow of financial capital.

The role of exchange rate changes in dominating international trade imbalances suggests that countries with current trade surpluses should have an appreciat­ing currency whereas countries with trade deficits should have depreciating currencies. Such exchange rate changes would lead to changes in international relative prices that would work to eliminate the trade imbalances like surplus or deficit.

In recent years, due to financial liberalisation, the volume of international trade in financial assets has far exceeded trade in goods and services. Moreover, there are some instances where countries with trade surpluses have depreciating currencies, whereas countries with trade defi­cits have appreciating currencies.

This is why a new approach to exchange rate determination has been devised. This is known as the asset approach or portfolio balance approach which explains the real-world events. This theory places a much greater emphasis on the role of the exchange rate as one of many prices in the global market for financial assets. In this context, we consider the asset approach to exchange rate determination in detail.

The asset approach to exchange rate determination emphasises financial markets for assets. Whereas the traditional view is that the exchange rate gets adjusted to equilibrate international trade in goods, the asset approach suggests that the exchange rate gets adjusted to equilibrate international transactions (flows) in financial assets.

Since prices of goods adjust slowly rela­tive to prices of financial assets and financial assets are traded continuously every day, the shift in emphasis from goods market to assets markets has important implications. Exchange rates will change any day as supplies and demands for financial assets of different nations change.

The asset approach assumes perfect capital mobility. This means that capital flows freely between countries in the absence of significant transactions cost or capital controls (in a liber­alised era).

In a world in which there are no barriers to international capital flows, covered interest arbitrage will ensure covered interest rate parity:

where i_d is the domestic interest rate and i_f is the foreign interest rate. Since this relationship will hold continuously, spot and forward exchanges as well as interest rates adjust instantane­ously in response to changing financial market conditions.

Paul R. Krugman has developed the asset approach to exchange rate determination. Krugman’s approach seeks to establish the relation between interest rate and exchange rate just as the PPP theory seeks to establish a relation between price levels and exchange rates. Two main attributes of assets remaining the same, viz., risk and liquidity, investors prefer to hold assets which offer the highest expected real rate of return.

This statement holds when investors have the option of investing those funds either within their domestic country or abroad. And the return on an asset, such as interest rate on foreign bonds, plays an important role in exchange rate determination.

The rate of return on a deposit of a particular currency is the interest rate or the amount of that currency an individual earns by lending a Unit of currency for a year. This is the variable which determines whether an individual will invest his funds within the domestic economy or abroad. He will always compare the rates of interest which prevail in two different countries, viz, the home country and foreign country, while deciding which asset (domestic or foreign) to buy.

Interest rates play an important role in the foreign exchange market because different de­posits traded in such a market pay different interest rates. In other words, each type of deposit pays a certain amount of interest depending on the currency in which it is denominated (i.e., whether in dollar or in pound or, now, in euro).

The dollar interest rate is simply the dollar rate of return on dollar deposits. Similarly, a foreign currency’s interest rate measures the foreign currency return on deposits of that cur­rency (such as the British pound).

The interest rate offered by a dollar and a British deposit will indicate how their dollar and pound values will change over a year. The rates of return offered by a dollar and pound deposits also depends on the expected change in the dollar/pound exchange rate over the year.

How can we find out which deposit offers a higher expected rate of return? To answer this question, we have to raise another question: If an American uses dollar to buy a pound deposit, how many dollars will he get back after a year? In order to answer this question we have to calculate the dollar rate of return on a pound deposit because we are comparing the dollar price today with its dollar price after a year.

A Simple Rule:

We know that the rate of depreciation of the dollar against the pound is the percentage change in the dollar/pound exchange rate. The dollar rate of return on British deposits is the British interest plus the rate of depreciation of the dollar against the pound. Thus, to translate the pound return on pound deposits in terms of dollar, we have to add the rate at which the pound’s dollar price rises over a year to the pound interest rate.

Suppose the pound interest rate is 5% and the expected depreciation of the dollar is 6% in one year. Thus the expected dollar return on pound deposits will be 11 %. Now, the expected rate of return on a pound deposit, measured in terms of dollar, is the sum of (1) the pound interest rate; and (2) the expected rate of dollar depreciation against the pound

or,

r_£ = today’s interest on one-year pound deposit

R_$/£ = today’s dollar/pound exchange rate (number of dollars per pound)

R_$^e /_£ = dollar/pound exchange rate to prevail a year from now

Here the superscript ‘e’ denotes people’s forecast of future exchange rate on the basis of current exchange rate.

This expected return has to be compared with the interest rate as one year dollar deposits r_$, in deciding whether dollar or pound deposits offer the higher expected rate of return.

The difference in the expected rate of return between dollar and pound deposits is equal to less the expression given by eqn. (1):

When this difference is positive, the dollar deposits yield the higher expected rate of return; when it is negative, the pound deposits yield the higher expected rate of return. The rate of return differential will be the same if returns are expressed in terms of pounds.

In order to measure the return on dollar deposits in terms of pounds we have to add to the dollar interest rate r_$ the expected depreciation of the pound against the dollar (or the expected rate of appre­ciation of dollar against the pound).

Thus, in terms of pounds, the return on a dollar deposit is:

We may now see what happens when a US resident buys a one-year UK bond. Suppose the exchange rate is $2 = £1. When the bond is purchased the US resident needs $2 to buy the bond. After one year the bond matures.

The bondholder receives the principal of £1 plus 10% interest (£ 0.10). Now the US resident wants to convert the pounds into dollars because he ultimately wants dollars for his family expenditure. [For this reason he must compare the dollar return from holding each bond.]

If in one year’s time the exchange rate has gone up from £1 = $2 to £1 = $ 2.10, i.e., if dollar depreciates in terms of pound the £1.10 proceeds from the bond are converted into dollars at the rate of $2.10 = £1. The dollar value of the proceeds- is $2.31 [the exchange rate (2.10) multiplied by the pound proceeds (£1.10)]. The dollar return from the UK bond is the percent­age difference between the dollar proceeds received after one year, and the initial dollar amount invested or 15% (approx.).

Alternatively we can determine dollar return from the UK bond by adding the UK interest rate to the percentage change in the exchange rate. The percentage change in the exchange rate is 5.

This is calculated as follows:

The dollar return from the UK bond equals the 10% interest paid in British pound plus the 5% change in the exchange rate or 15%. In this example, pound appreciates against dollar. When the pound increases in value, Ameri­cans holding pound denominated bonds earn a higher return on those bonds than the pound interest rate.

If the pound depreciates against the dollar, so that the pounds received at maturity are worth less than the pounds originally purchased, then the dollar return from the UK bond is less than the interest rate of the bond. If the bond depreciates 5% the dollar return is just 5% (interest rate 10% minus the exchange rate change 5%).

Calculating the Domestic Currency Return on a Foreign Bond:

We calculate the domestic currency return from a foreign bond by adding the foreign interest rate plus the percentage change in the exchange rate:

Domestic currency return = foreign interest rate + percentage change in exchange rate

This point may now be explained further. Thus the return on a dollar deposit is the same whether we measure the return in terms of dollar or pound, as long as we measure it in terms of a single currency.

Comparison with the Monetary Approach:

Within the family of asset-approach models, there are two basic groups: the monetary ap­proach and the portfolio-balance approach. In the monetary approach, the exchange rate be­tween any two currencies is determined by relative money demand and money supply between the two countries.

Relative supplies of domestic and foreign bonds are less important. The portfolio balance approach allows relative bond supplies and demand as well as relative money market conditions to determine the exchange rate.

The main difference between the two approaches is that the monetary approach assumes that domestic and foreign bonds are perfect substitutes whereas the portfolio balance approach assumes these to be imperfect substitutes. If domestic and foreign bonds are perfect substitutes, then demanders are indifferent about the currency of denomination of the bond as long as the expected return is the same.

In this case, bond holders do not receive a premium to hold foreign bonds. So he would hold foreign bonds along with domestic ones. Thus means that there is no risk premium, and uncovered interest rate parity holds in the monetary approach.

With imperfect substitutability demanders have preferences for distributing their portfolios over the assets of different countries. This means that asset holders have a desired portfolio share for any particular country’s asset due to the portfolio diversification. If the supply of one coun­try’s assets increases, they will hold a greater proportion of that country’s asset only if they are compensated.

So a premium has to be paidion these assets. In general, then, the portfolio balance approach has risk premium in the forward exchange rate that is a function of relative asset sup­plies. As the supply of A’s asset rises relative to B’s there will be a higher premium on A’s assets.

An implication of this premium is that uncovered interest rate parity will not hold because risk premium does not exist in the monetary approach. The reason is investors do not know whether they hold country A or country B bonds and in what mix these are held.

It appears that the portfolio balance approach is more relevant if we doubt basic assumption of the monetary approach viz., of perfect substitutability of assets internationally. In such cases we would view the exchange rate as being determined by relative supplies of domestic and foreign bonds as well as domestic and foreign money.

The portfolio balance approach assumes that assets are imperfect substitutes internation­ally. The reason is that investors perceive foreign exchange risk to be attached to foreign cur­rency denominated bonds. As the supply of domestic bond rises relative to foreign bonds, there will be an increased risk premium as the domestic bonds will cause the domestic currency to depreciate in the spot market. If the spot market exchange rate depreciates today and if the expected future spot rate remains unchanged, the expected rate of appreciation (depreciation) over the future increases (decreases).

In terms of Krugman’s asset approach the exchange rate at which the market settles is the one that makes market participants content to hold existing supplies of deposits of all curren­cies. When the market participants voluntarily hold the existing supplies of deposits of all currencies, the foreign exchange market is said to be in equilibrium.

To be more specific, the foreign exchange market is in equilibrium when deposits of all currencies offer the same expected rate of return. This condition is known as the interest par­ity condition. In other words, the interest parity condition states that the expected return on deposits of any two currencies will be the same when measured in the same currency. Eqn. (2) shows the difference between the expected return on the two assets in terms of dollars. The expected rate of return are equal when

This is known as the interest parity condition, i.e., the condition under which similar finan­cial assets have the same interest rate when measured in the same currency. For this reason we find a close relationship among international interest rates. To be more specific, the return or interest rate tends to be the same on similar bonds when returns are measured in terms of the domestic currency. This is called interest rate parity (IRP).

Interest rate parity is the financial asset version of purchasing power parity. Similar finan­cial assets have the same return (in percentage terms) when that return is computed in terms of one currency. Interest rate parity establishes a relationship among the domestic interest rate, the foreign interest rate and the expected change in the exchange rate.

Domestic interest rate = Foreign interest rate + expected change in exchange rate.

In our example the US bond pays 15% interest; the UK bond offers 10% interest in pounds. If the pound is expected to appreciate 5%, the UK bond offers US residents an expected dollar return of 15%.