Deduction of the Properties of Indifference Curves (IC)

In this article we will discuss about the deduction of the properties of Indifference Curves (IC).

The first property of an IC is that it is negatively sloped, i.e., it slopes downward towards right. This property follows from axiom of dominance which implies that both the goods are of MIB type.

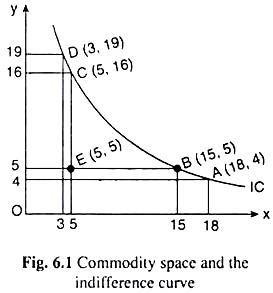
For, if, in the case of any two points A and B in the commodity space, the quantity of good X is larger at B while that of good Y remains the same or it is also larger at B, then the consumer cannot be indifferent between these two points, because here the level of utility would be higher at point B than at point A on account of the MIB assumption.

However, the consumer may be indifferent between these two points, i.e., the points A and B may lie on an IC, if at point B as compared to point A, x is larger and y is (appropriately) smaller. This is because here point B’s gain in utility from a larger x would be aptly compensated by its loss in utility from a smaller y.

However, by how much y should be less at point B so as to make the consumer indifferent between A and B would be determined by none else than the consumer himself—this is a matter of his personal preference.

In this case, point B would lie on the same Indifference Curves IC as A but further downwards towards right (since at B, x is larger and y smaller). In other words, an IC would be negatively sloped. The negative slope property of the ICs may also be established with the help of Calculus.

Let us suppose that the ordinal utility function of the consumer is:

Now suppose that the consumer moves from a point (x,y) in the commodity space to another very close point (x + dx, y + dy).

As a result, the change in his utility level (dU) would be obtained by taking the total differential of (6.6):

Now, if the point (x,y) and (x + dx, y + dy) are situated on the same IC, then the difference in U between these points would be zero, i.e., then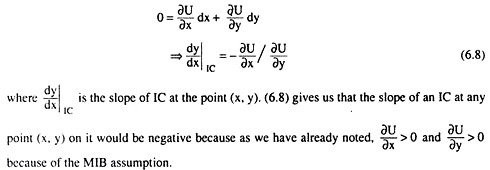

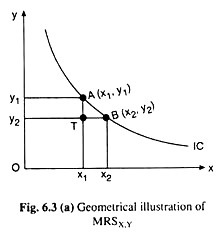
The second property of an IC is that it is convex to the origin. This property directly follows from axiom (vi) which states that MRS _x, y would be diminishing as the consumer has more of X and less of Y along an IC. For,  MRS_{X Y} at any point on an IC is equal to its numerical slope at that point.

So the assumption of diminishing MRS_X,Y implies diminishing numerical slope of the IC as the consumer has more of X and less of Y, i.e., as the consumer moves downward towards right along the IC. This immediately implies that ICs are flatter down­wards, i.e., they are (strictly) convex to the origin like the curve shown in Fig. 6.1 or 6.3(a).

Alternatively, Indifference Curves ICs are convex to the origin owing to axiom of convex preference.

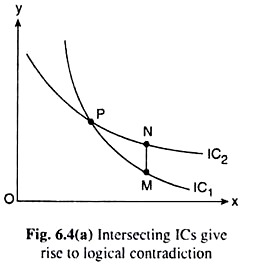
The third property of the ICs in our list is that they are non-intersecting curves. To prove this let us assume, for the sake of argument, that two ICs have actually intersected as shown in Fig. 6.4(a), at the point P. Let’s take any two points M and N on IC₁ and IC₂ such that M lies vertically below N.

The following can be obtained in Fig. 6.4(a). Since the points M and P lie on the same IC, viz., IC₁, the consumer is indifferent between the points M and P is obtained, i.e.,

M ~ P ….(6.9)

Again, the points P and N lie on the same IC, viz., IC₂.

So the consumer is indifferent between the combinations P and N, i.e.,

we have P ~ N …..(6.10)

Therefore, (6.9) and (6.10) gives:

M ~ P ~ N …..(6.11)

and by virtue of axiom of transitivity of preferences, M ~ N ……(6.12)

But the combination M lying vertically below the combination N, has the same quantity of good X, but a smaller quantity of good Y. This gives, because of MIB axiom of dominance, that the combination N is strictly preferred to combination M, i.e., N > M …..(6.13)

From the analysis, if any two ICs actually intersect, then (6.12)is obtained because of the transitivity axiom and (6.13) because of the MIB axiom. Since (6.12) and (6.13) are contradictory results, it may be concluded that our logical system breaks down, i.e., arriving at a logical contradiction, if any two ICs happen to intersect. Hence, ICs are non-intersecting curves.

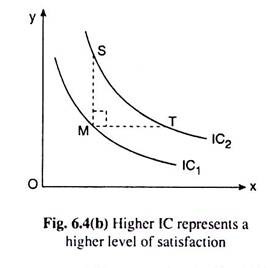
Lastly, the fourth property of the ICs is that a higher IC represents a higher level of utility. As seen now with the help of Fig. 6.4(b), this property follows from the MIB assumption. In Fig. 6.4(b), M is any point on the lower IC, viz., IC₁. It may be seen that there would be obtained a large number of points on the higher IC₁ viz., IC₂, that contain more of either one or both the goods than M on IC₁.

In fact, these points are the points on IC₂ that lie on the ST segment of the curve. So, because of the MIB assumption, level of utility at any point on the arc ST of IC₂ is higher than that at the point M on IC,. Now, all the points on an IC represent the same level of satisfaction. Hence, it may concluded that a higher IC represents a higher level of satisfaction.

In the analysis, it can be seen how the properties of the ICs from the axioms of preferences may be deduced.

Henceforth, proceeding with the analysis of the IC theory of consumer behaviour by assuming that the ICs possess the properties. Some of the applications of the theory may be illustrated. There the axioms may change leading to changes in the properties of the ICs.