Essay: Foreign Exchange and Economic Development

Foreign trade enables on LDC to go beyond its Antarctic PPF. Trade, properly conducted, can ease the problem of shortage of foreign exchange faced by a country, and this can have dy­namic consequences. Prima facie, a larger inflow of foreign exchange can enable an LDC to break the vicious circle of low savings and low growth.

Growing foreign exchange can be used to import either or consumer goods, while devoting domestic resources to the production of capital goods. In either case, it is possible to increase investment and accelerate the rate of growth without curtailing consumption.

Thus foreign exchange can be used to add to the sup­ply of financial resources by supplementing inadequate domestic saving. Foreign exchange earned through exports plays another important role in the growth proc­ess. Foreign exchange enables an LDC to imports those machines and capital goods which it cannot produce domestically.

These two roles of foreign aid- viz.,

(1) Augmenting domestic savings and

(2) Enabling import of essential capital goods.

Both are captured by the so-called two-gap model of eco­nomic growth, developed by H.B. Cannery and Bruno in 1962. It has been subsequently modified by Mckinnon in 1964. This is a fixed price model. It is also a non-shift able model, implying that foreign resources and domestic resources are perfect compliments of each other, not substitutes in any way. We start with the Chenery model and then switch over the Mckinnon model.

Foreign saving (F) can finance the amount by which domestic investment exceed domestic saving (5), so that, F = I – S. Alternatively, foreigners can finance the trade deficit, i.e., the excess of imports over exports, F = X-M. From the standard national account system it fol­lows that I- S is always equal to M-X.

We know from national accounts that

Y = C + I + G + X – M … (1)

Moreover, all income must be consumed (C), paid in taxes (T), or retained as prevailed saving (S_p), or, Y= C + T+ S_p. Combining these two identities, and rearranging terms, yields

(T-G) + S_p = I + X – M … (2)

Since T- G is equal to government saving, the left hand side of equation (2) is equal to total domestic saving, 5. Substituting this in equation (2), and rearranging terms, yields the identity

I – S = M – X … (3)

This is the essence of the two-gap model of foreign aid.

Foreign saving has two components- official saving and private saving. The major portion of official saving is on concessional terms. Such saving is made available either as grants (outright gifts) or as “soft” loans, bearing lower interest rates and longer repayment periods than would be available in private international capital markets.

Governments and interna­tional agencies also make some loans on commercial terms (”hard” loans). Most governments and multilateral organisations (such as the World Bank and regional development banks) make both soft and hard loans to developing countries. Concessional flows technically are called official development assistance (ODA) but popularly are called foreign aid.

Aid is also sub­divided into bilateral aid, given directly by one government another, and multilateral aid, in which the funds flow from governments to international agencies like the United Nations, the World Bank, and the regional development banks, which in turn grant or lend the fund’s to recipient LDCs developing countries. Finally, aid can take the form of technical assistance, the provision of skilled personal to LDCs, or capital assistance, the provision of finance or com­modities, mainly food, as under PL 480 and PL 665.

The Mckinnon Model:

The Mckinnon model throws light on some issues in the dynamics of foreign exchange and trade.

There are two kinds of capital, domestic and foreign, and these are required in fixed propor­tions to produce society’s output

Y=mm {_aK_d,_bK_s] … (1)

where K_d and tf/are the available supplies of domestic and foreign capital, and Y is national income (which is the sum-total of both consumer goods and capital goods produced in the economy). Assuming full utilisation of existing capital in the economy, we have

Y=_aK_d = bK_f … (2)

The total annual savings, S, may be expressed as

S = sY … (3)

The maximum annual export capacity, E, is

E = eY … (4)

Here Y is an index of the country’s capacity to produce quality goods which can be ex­ported.

The total investment I or the net addition to the total capital stock of the economy which is made in an accounting year, i.e.,

I = ∆K = ∆K_d + ∆K_f = I_d I_f

where I_d = ∆K_d and I_f = ∆K_f

If there is full utilisation of capital stock (that is, given Y = _aK_d – _bK_f) we have

I = I_f + I_d =b 1/(a b)I(a +b)I_f = b/v I_f …(5)

where v = ab/(a+ b) the capital-output ratio.

Let F denote the volume of foreign capital transfer that takes place in a year in the form of foreign exchange received (as loan and/or aid). It is quite obvious that the maximum amount of foreign exchange that can earned in a year is

(e + f)Y, where f ≡ F /Y.

Hence from equation (5)— I=b/vI_f = — l_f, the maximum value of (b/v) is given by (+f)Y .This is indeed the maximum possible value of investment subject to the foreign capital constraint. But this may not be realised due to inadequate saving. Since savings S = sK, consumption C = (1 – s) Y. This means that the total investment cannot exceed sY (domestic savings) plus fY (the amount which can be purchased with foreign exchange). This means that investment has to be less than (s +/) Y. This is the savings constraint. Combining the two constraints we get

I = min {(s + f)Y, b/v(e + f)Y} … (6)

The growth rate of the economy, g, equals AY/Y where AY is the change in income during the year.

From (2) and (5) we get:

g = (v/y)I

If we substitute 1 from (6), we get

g = min {v (s+ f), b (e+ f)} … (7)

Thus the growth rate depends on which constraint is binding. If, for instance, the foreign exchange (capital) constraint is binding, i.e., (b/v) (e + f) Y < (s + f) Y, then g = b (e + f)

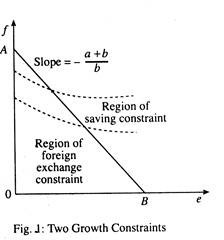
The two-gap model of growth can now be repre­sented diagrammatically. In Fig. 1 to the left of the line AB the foreign exchange constraint is binding and to its right the saving constraint is binding. It is quite obvious that AB is the locus of all values of e and/that satisfy v (s + f) = b (e + f).

If the foreign exchange constraint exists, increased exports will not raise the growth rate. However, in an LDC like India suffering from foreign exchange cri­sis, export and growth rate are positively related. An increase in F invariably increases the growth rate, al­though its effectiveness is greater to the left of AS. Until F comes in the form of outright grant, it has to be re­paid in the future.

So there is need to explore the possibility of raising the growth rate through other measures. One way of raising the growth rate quickly is to adopt two measures simulta­neously, viz., raising the country’s capacity to export, e and to simultaneously to increase the savings rate, s.

Implications of the Model:

No doubt the two-gap model is based on some rigid assumptions. Yet it brings into focus the relation between the growth rate and savings. There is no need to underestimate the positive contribution that saving makes to growth rate. At the same time we should not surprise by the fact that growth rates stagnate even if the rate of savings (s) increases.

If, for instance, there is a shortage of foreign capital equipment, .then from equation (7) g = min {V (5 + f), + f)} we see that g is totally unresponsive to increases in s. An increase in s causes an accumulation of inventories, while leaving g unaffected.

Thus rising savings rates may not promote faster growth. Even if the stock of domestic capital increases, it will remain unutilized, if the foreign capital constraint is effective. As a result the capital-output ratio (v) will rise but g will remain constant. Three comments may be made in this context.

Import Substitution:

The two-gap model is related to the policy of import substitution, i.e., producing capital goods which were earlier imported. This strategy, by shifting the foreign capital constraint, would raise the growth potential of an LDC.

In this model industrialisation is equated to a rise in the economy’s capacity to export (e). If the foreign exchange constraint is effective, then faster industrialisation (by raising exports) accelerates the growth rate of an economy. The argument in favour of industrialisation becomes stronger if the terms of trade between primary industries and industrial goods have a secular tendency to decline.

Terms of Trade Deterioration:

If terms of trade deteriorate, a larger availability of foreign exchange is likely to do more harm than good to an LDC, the aid-receiving country. There are various situations where a transfer of commodities or aid results in a decline in the welfare of the recipient. A loss of welfare occurs as a consequence of terms of trade deterioration, as has been pointed out by J. N. Bhagwati.

Consumption Leakage and Debt Trap:

In this model investment cannot be stepped up without increasing F. However, in reality F is not under full control of the planners and policy makers of an LDC. However, if the available foreign exchange is used to increase consumption or is spent on non-productive capital, then more foreign exchange will be needed in future not only to repay the loan but also to import consumption goods. In other words, the economy will fall in a debt trap which reduces national welfare by driving the country inside the PPF.

A country has to curtail its domestic consumption latter to be able to generate export surplus with which to service the debt. In low-income countries there is always an extra temptation to use aid to buy consumer goods. So the possibility of a debt trap is a threatening one. There is no guarantee that F will automatically promote social welfare.