Study Notes on the Public Expenditure Function | Econometrics

The below mentioned article provides a study note on the public expenditure function.

In order to discharge various functions, the Government has to incur expenditure for different purposes. As the public sector goes on increasing, the amount of expenditure for various development activities also increases. Thus both the expansion of public sector and public expenditure move together in the same direction.

In other words, as the public sector increases the activities of the government go on increasing. This is concerned with Wagner’s law of rising public expenditure. The proxy for public sector is Gross Domestic Product.

The relationship between gross domestic product and Public expenditure can be specified as follows:

Y = f [X]

Where

Y = Public Expenditure

X = GDP [Gross Domestic Product] or Income

In order to test the empirical validity of Wagner’s law of rising public expenditure, the elasticity of public expenditure with respect to income needs to be estimated.

The elasticity of public expenditure with respect to income is the ratio of the proportionate change in public expenditure to the proportionate change in income as shown below:

dY /Y / dX / X = dY / dX. X / Y

If the value of this elasticity is more than unity, then Wagner’s law is said to be operating. If it is less than unity, then Wagner’s law is said to be not operating. Thus, on the basis of numerical value of income elasticity of public expenditure the empirical validity of Wagner’s law can be understood.

This will be tested using different methods:

[1] Between two points of time

[2] Over a period of time.

Between two points of time, the following formula will be used to test the empirical validity of Wagner’s law:

e_Y.X = Y_t – Y_t-1/Y_t-1/X_t –X_t-1/X_t-1

Where

Y_t = Public expenditure in current year

Y_t-1 = Public expenditure in previous year

X_t = GDP in current year

X_t-1 = Gross Domestic Product in previous year

The above formula is confined to two points of time. The validity of Wagner’s law can also be examined over a period of time as well. For this the regression analysis will be used. Of different forms of the regression equations, linear and log- linear forms of regression equations will be used to test the validity of law.

Linear Demand Function for Public Expenditure:

Specification of a linear demand function for public expenditure will be as follows:

Y = b₀ + b₁X + error ……………….(92)

Where

b₀ is the trend value [estimated value] of public expenditure in the absence of income

b₁ is marginal propensity to spend i.e., dY/dX, whose value will always be positive.

The values of b₀ and b₁ will be estimated by OLS [Ordinary Least Squares] method with specific assumptions.

The elasticity of Y with respect to X will be estimated as follows.

e_Y.X = dY/dX. X/Y

= b₁. X/Y

Here, the mean value of X and Y or total of X and Y or the individual values of X and Y will be used. In the empirical studies, the mean values of X and Y will be used. Therefore, this is referred to as an average elasticity of public expenditure with respect to income.

= b₁. mean of X/mean of Y

If its value is more than unity, then Wagner’s law is said to be in operation. It should be noted that the elasticities vary from point to point if the individual values of X and Y are used in evaluating the expenditure elasticities.

If the linear demand function for public expenditure is not suited to time series data, then other forms of regression equations have to be attempted. The log-linear form of regression equation will be estimated in empirical studies to know the empirical validity of Wagner’s law.

Log-Linear Demand Function for Public Expenditure:

The specification of a log-linear demand function for public expenditure will be as follows:

log Y = log b₀ + b₁ log X + error …………………(93)

The above function will also be estimated by OLS method. The derivative of log Y with respect to log X is b₁, which gives directly the value of elasticity of public expenditure with respect to total income. If the value of b₁ is more than unity, then the proportionate change in Y will be relatively higher than the proportionate change in X implying that Wagner’s law of rising expenditure is said to be operating.

If it is less than unity, then the proportionate change in Y will be relatively lower than the proportionate change in X. If it is unity then the proportionate change in Y will be equal to the proportionate change in X. If the elasticity is less than or equal to unity, then Wagner’s law of rising expenditure is said to be not operating.

Public Expenditure Function-Estimates of Economic Relationships:

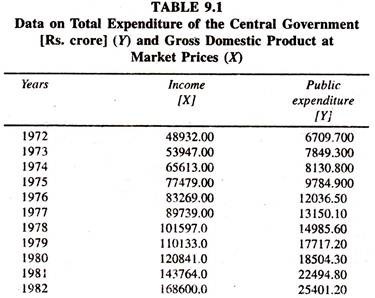
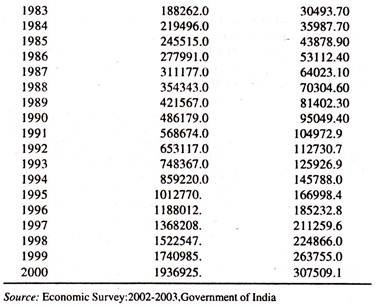
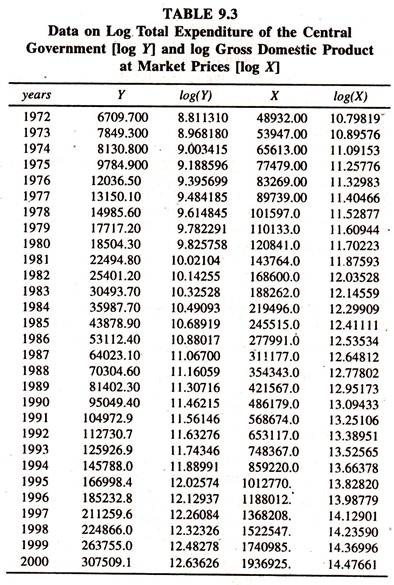
The data [Table 9.1] on total expenditure of the central government [Rs. crore] (Y) and gross domestic product at market prices (X) are considered to fit the regression models [Both the linear and log linear] to examine the empirical validity of Wagner’s law.

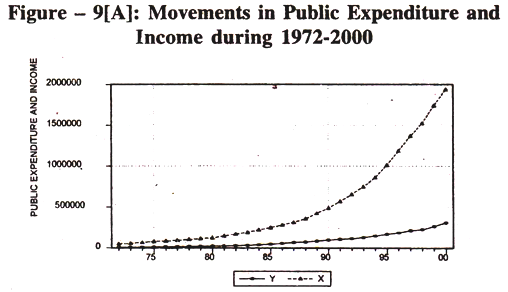
Visual Plot:

The Public expenditure and income series move together in the same direction [Figure – 9[A]]

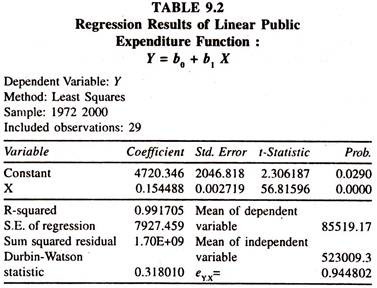
The regression results of the linear public expenditure function [Table 9.2] show that the regression coefficient of income, marginal propensity to spend, is significantly positive.

The average elasticity of public expenditure with respect to income [estimated at the mean values of Y and X :0.154488(523009.8/85519.17)] is 0.9448 showing that a one percent increase in income leads to increase public expenditure by 0.9448 percent. Since the value of elasticity in the linear regression is close to unity, Wagner’s law of public expenditure is said to be not operating during the period under consideration so far as the data are concerned.

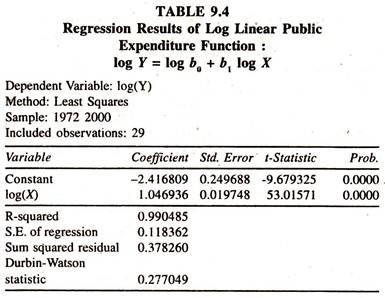
The regression results of the log linear public expenditure [Table 9.4] based on the data given in table 9.3 show that the regression coefficient of log income, which is constant income elasticity of public expenditure, is significantly unity. Out of this, it can be inferred that a one percent increase in income leads to increase the public expenditure by 1.047 percent.

In the log linear form of regression equation also, the value of income elasticity of demand for public expenditure is unity, evincing the fact that wagner’s law is not operating in a strict sense. In empirical studies, the per capita real public expenditure and per capita real income variables [real ratio variables] can also be considered for capturing the changes in population and prices.