Single Firm’s Demand Curve for Capital

Keynes defined the marginal efficiency of capital (MEC) as the rate of discount, e, that will just equate the present value of the flow of receipts a capital good (such as a machine) generates equal to its purchase price.

If the future cash flow or monetary return that can be obtained (expected) from a piece of capital is assumed to remain uniform throughout we can cal­culate the MEC by applying the following simple formula:

C = R/e

where C is the purchase price of the piece of capital, R is its constant flow of gross returns and e is the unknown value of MEC.

Now we can easily solve for e by using this formula:

e = R/C

If we assume that a firm is having a large num­ber of capital equipment and is making a decision, at the margin, to acquire one extra unit of capital, we may call the e associated with this marginal addition to the firm’s stock of capital the MEC.

Here e is the efficiency of any unit of capital, and MEC is the ef­ficiency of the marginal unit. What is true of a firm is equally true of society. So we can refer to MEC for the whole economy.

We have noted earlier that the value to the firm now of a flow of future cash flows is its present value while the purchase price is the cost to the firm now of the capital that produces that flow of receipts. While the former is the addition to revenue made by an ex­tra cost of acquiring the piece of capital the latter is the extra cost of acquiring the piece of capital.

Ac­cording to the famous marginal productivity theory of income distribution a profit-maximizing firm will go on adding units of capital so long as its marginal revenue product (MRP) exceeds it cost. Thus a firm will go on adding to its existing stock of capital as long as the present value of the flow of receipts from the marginal units exceeds the purchase price.

The value of e is the rate of discount which makes the two (R) and (C) equal. But we calculate the present value on the basis of the market rate of in­terest (r). (This is exactly what we have done earlier in this section).

Thus, when MEC is exactly equal to r, the present value of future cash flows from the marginal unit of capital equals its current purchase price (or acquisition cost). When this happens the firm’s capital stock is said to be in equilibrium and firm would no longer consider it worthwhile to add another unit of capital.

An interesting question that arises at this stage is the following: How does the firm take decision regarding whether or not to acquire (buy) one extra unit of capital?

The usual method used by modern business firms is to use the market rate of interest to arrive at the present value of the gross return. Then, in the next step, it has to be compared with the purchase price of the piece of equipment. A simple example, may make the point clear.

Let us suppose that a firm can buy a machine for Rs. 8,000. It is expected to yield Rs. 1,000 per annum, net of all non-capital costs, for an indefinite period. Also suppose that the market rate of interest at which it can borrow (and lend) money is 10 per cent. Thus, the present value of the future cash flow generated by the machine (i.e., the capitalized value of the machine) is R/r = Rs. 1000/0.10= Rs. 10,000.

On the other hand the present value of Rs. 8,000 today is (obviously) Rs. 8,000. The firm can make a gain if it purchases the machine for Rs. 8,000 to derive an income of Rs. 10,000. We may alternatively suppose that the firm is left with two options—either to buy the machine or lend the money (Rs. 8,000) at 10 per cent interest.

The firm would prefer to buy the machine because, by doing do, it can get an income of Rs. 1000. On the other hand if it lends the money at 10 per cent interest, it gets, at the end of a year, a sum of Rs. 800 as interest.

Thus, it is quite clear that the first option is better than the second one.

So as a general rule a profit- maximizing firm will purchase a capital good like a machine if the following condition holds:

R/r > C

where R is the infinite stream of future (gross) cash flows. The term R/r is the present value of the stream of gross cash flows generated by the capital good, i.e., the capitalized value of the machine.

It will, therefore, be worthwhile, on the part of a profit-maximizing firm, to purchase a capital good as and when the present value of its future stream of gross returns exceeds the purchase price of the good.

The above inequality may also be expressed in the an alternative way:

R/C > r

But R/C is the MEC. So we obtain the following rule of investment decision at the micro level, i.e., at the level of an individual firm: it is always profitable for a firm to acquire extra units of capital whenever its MEC exceeds the market rate of interest.

Looked at from this angle, MEC measures the return on an extra (marginal unit of capital to the firm, while r is a measure of the opportunity cost of capital (always assuming that the firm can borrow and lend at the existing market rate of interest, which is 10 per cent in our example).

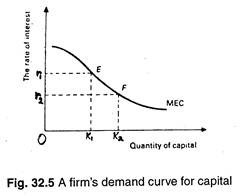
A firm’s MEC curve is shown is Fig. 32.5. It is a schedule that relates the efficiency of each additional rupee’s worth of capital to the size of the capital stock. On the horizontal axis we measure the value of the firm’s capital stock. On the vertical axis we measure the money value of the product of capital, expressed in terms of percentage yields on that capital.

The MEC curve is downward sloping, as stated earlier, due to the operation of the law of diminishing returns. .Thus, in Fig. 32.5 when the stock of capital is k₁ the MEC is r₁. When the stock of capital increases to k₂ the MEC falls to r₂ and so on.

In fact, the MEC curve is known as the firm’s demand curve for capital. It shows the amount of capital that a firm would choose to employ at different costs of employing it (i.e., at different rates of interest). The MEC curve is indeed the demand curve for capital of a firm because it shows how much capital the firm will demand at different prices, or yields, of capital.

We may note here that the cost of capital is the market rate of interest, i.e., the interest that the firm has to pay to borrow funds to acquire capital (or, for a firm that has generated funds internally, the cost of capital is the rate of interest that could be earned by lending them elsewhere).

Keynes pointed out that so long as the MEC ex­ceeds the rate of interest, net return from a project will be positive. So the firm will employ more capital. But as MEC gradually falls, it will ultimately be equal to r and the firm’s stock of capital will be optimum. This point may also be illustrated diagrammatically.

Sup­pose in Fig. 32.5 the rate of interest (the cost of capital to the firm) is r₁. Now the firm will certainly employ all capital upto k₁ because the MEC is greater than the rate of interest. At the same time, it will not be profitable for the firm to employ, say, units of cap­ital because the MEC of the k₂-th unit of capital is less than the rate of interest.

In a like manner, it will not pay the firm to employ any capital in excess of k₁. Hence k₁ represents the optimum stock of capital of the firm, when the rate of interest is r₁. Thus the equi­librium amount of capital of a profit-making firm is that at which the MEC is exactly equal to the rate of interest.

There is another way of establishing the funda­mental principle stated above. In our previous ex­ample, a machine producing children’s toys was sup­posed to generate a yield of 10 per cent. If the market rate of interest is 10 per cent or less, it will be profitable to buy the machine: If the rate of interest is more than 10 per cent, it will not be profitable to buy or install it.

The Economy’s Demand Curve for Capital:

By adding up the MEC schedules of individual firms we arrive at the MEC schedule of society. So like the downward MEC schedule of a firm the MEC schedule for the society as a whole is also downward sloping.