The following article will guide us to learn about how to calculate Marginal Efficiency of Capital (MEC) and investment.
Normally, we conceive of an investment project as the purchase of an asset which yields a stream of returns (cash flows) over time. (R1, R2,…., Rn) where the last return includes the scrap value of the income-earning asset or capital goods like a machine.
Suppose, now, that we are given the purchase price or cost of a capital good, denoted by C and the income stream to be produced by the machine as R1, R2……, Rn. What we want to find out here is the rate of discount that will make the present value of the income steam produced by a machine, say, just equal to its cost. Or, in other words, we want to find the value of the discount rate e for given values of C and R1, R2, Rn.
The formula is:
ADVERTISEMENTS:
C = R1/(1 +e) + R2 (1 + e) 2 + Rn/(1 + e) n
This can be reduced to a simple expression C = R/e or e = R/C if we assume that the annual revenue is uniform or R1 = R2-……….. = Rn. The rate of discount found in this way is denoted by e to distinguish it from the market rate of interest r. Here we assume that no revenue is received until the end of the first period and that all investment expenditures occur at the beginning of the project.
An Example:
For a numerical illustration, assume that the purchase price of a capital good is Rs. 427.02. It is also expected to produce an income stream of Rs.100 at the end of each year for a period of five years.
ADVERTISEMENTS:
Substituting these figures in the above equation we get:
Rs. 427.02 = Rs.100/(1 + e) + Rs.100/ (1 + e)2 + Rs.100/(1 + e)3 + Rs.100/(1 + e)4 + Rs.100/(1+ e)5
Solving this equation we get the value of e as 5.5%.
This calculation can be done for any other price of the above machine. For a given income stream, the higher the price of the machine, the lower will be the value of e. For example, if C=Rs.485.35, e would be a mere 1%. But if C=Rs.299, e would be 20%.
ADVERTISEMENTS:
Here e is called the marginal efficiency of capital (MEC) by Keynes. It is that rate of discount that will make the present value of the returns from a capital asset during its economic life (which depends on the rate of depreciation) exactly equal to its market price or acquisition cost.
Now, by comparing this MEC with the current market rate of interest, r, we can at once assess whether a new investment project will be profitable or not. For example, if r = 6%, the investment project is not worth its while and if r = 5%, it would be considered profitable. In fact, by simply finding out the difference between the MEC and r, we can calculate the net rate of return on the capital asset after making allowance for all costs, including the interest cost of the funds tied up in the capital good over its life and the depreciation cost of the asset.
Then, if r = 6% and e = 5.5% purchase of the capital good promises a net return of 0.5% over and above all costs. But, the fact remains that major changes in interest rates are often associated with changes in investment.
Putting it all together:
We may now see how the three elements — C, R and e — fit together.
The following points are worth noting here:
1. An improvement in the business outlook that causes a business to revise upward his estimate of the expected income flow from a capital good will, given its unchanged price, raise the MEC of that good.
2. Alternatively, if the income flow expected from an asset remains unchanged, a fall in its price will raise its MEC. (For instance, if C = Rs.299, e will be 20%).
3. A fall in r does not affect the MEC of that good. But if r > MEC before the fall and if MEC > r after fall, the purchase of the capital good, which previously appeared unprofitable, will now be worthwhile.
ADVERTISEMENTS:
The MEC Schedule:
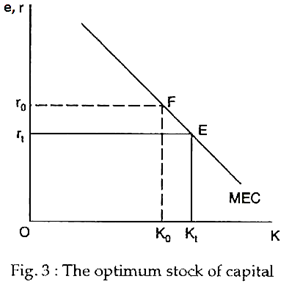
If we assume that at any given time there are many possible investment projects (additions to capital stock) yielding high return (MEC) and more yielding low return (MEC), we can graphically show the relationship between optimal capital stock and e as in Fig. 3. This relationship is the marginal efficiency of capital schedule.
The firm should acquire all investment project for which e > r, indicated by Kt in Fig. 3. In fact, firms would always like to add to their existing capital as long as the marginal efficiency of that capital exceeded the interest rate. If we assume that capital is subject to diminishing returns, then the MEC will fall as the stock of capital increases. The capital stock will thus be of equilibrium size when MEC equals the rate of interest.
ADVERTISEMENTS:
So, it is clear that the equilibrium (optimal) size of the capital stock varies inversely with the rate of interest. Thus, a fall in the rate of interest from r0 to rt leads to an increase in the volume of investment by K0 — Kt.
Aggregate Investment:
Now individual firms’ MEC schedules can be aggregated to get relationship between the interest rate and aggregate investment function. In macro economics we are more interested in the latter than in the former.