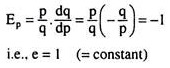6 Main Types of Demand Curves (With Diagram)

Some of the important types of demand curves are listed below:

Type # 1. Negatively Sloped Straight Lines Demand Curves:

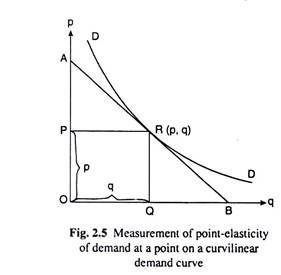
It is evident that the value of e at any (p, q) point on a curvilinear demand curve and the value of e at the same (p, q) point on a straight line demand curve—which is a tangent to the former demand curve at the said point—are identical.

For example, the value of e at the point R (p, q) on the curvilinear demand curve DD in Fig. 2.5 and the value of e at the same point, R, on the straight line demand curve AB which is a tangent to DD at the point R, are both equal to RB/RA.

In other words, the value of e at any point on a curvilinear demand curve may be shown to be equal to the value of e at the same point on an appropriate negatively sloped straight line demand curve. That is why, from the point of view of elasticity measurement,it shall be assumed that the demand curves are negatively sloped straight lines.

Suppose, such a straight line demand curve is:

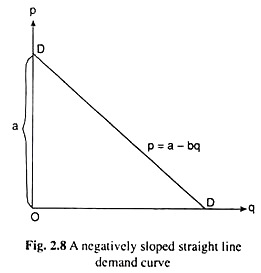
P = a – bq ; a > 0, b > 0 (2.9)

The slope or the straight line (2.9), as shown in fig. 2.8, is dp/dq = -b < 0 and its vertical intercept is a > 0.

Now, at any particular (p,q) point on this demand curve, it is obtained:

 

 

 

Here e is the numerical value of the coefficient of price-elasticity of demand at any (p, q) point on the straight line demand curve (2.9).

Type # 2. Iso-Elastic Demand Curves:

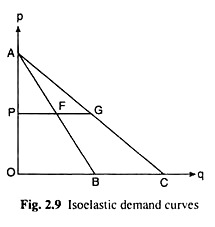
By definition, if the elasticities of demand at each price are equal on two different demand curves, then the two demand curves are said to be iso-elastic.

Now, from (2.10), it is obvious that if the vertical intercepts (here intercept on the p-axis = a) of any two different straight line demand curves are the same then, at any price (p), the value of e on these curves would be identical, and so, these two demand curves would be iso-elastic.

For example, in Fig. 2.9, AB and AC are two straight line demand curves. The vertical intercepts of both these curves are OA. Therefore, from (2.10) it is obtained that, at any particular price OR i.e., at the points F and G on the demand curves AB and AC, the values of e are identical. Arriving at the same result with the help of simple geometry. At the point F on the line

Therefore, at any particular price OP, the values of e on the demand curves (lines) AB and AC (at the points F and G, respectively) have been obtained to be identical. Therefore, here the two demand curves AB and AC are iso-elastic.

Type: 3. Parallel Demand Curves:

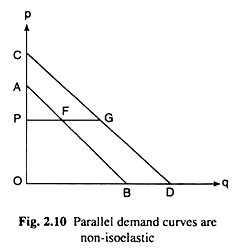
Parallel demand curves, it should be remem­bered that even if the slopes of two straight line demand curves are equal, i.e., even if the two such demand curves are parallel, they are not iso-elastic. For example, in Fig. 2.10, suppose that AB and CD are two straight line demand curves parallel to each other. Therefore, the slopes of these two curves (lines) are equal.

Now, at any p = OP, it is obtained:

Therefore, the parallel straight line demand curves are not iso-elastic. At any particular price, of the two parallel straight line demand curves, the one nearer the origin (here AB) would have a higher e than the other (here CD).

Type: 4. Intersecting Demand Curves:

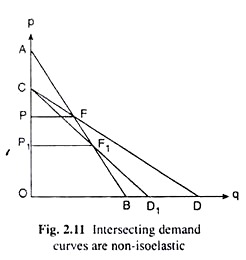
If any two straight line demand curves intersect each other, then, at any particular price of the good concerned, the steeper line would have a lower e and the flatter line would have a higher e. The point is established with the help of Fig. 2.11 where, at the price p = OP, the straight line demand curves AB and CD have intersected at the point F. Of the two demand lines, AB is the steeper line and CD is the flatter line.

Now, in Fig. 2.11, at the price OP and at the point F, having

e on the line AB is e₁ = FB/FA = OP/PA

and e on the line CD is e₂ = FD/FC = OP/PC

Since, PA > PC, and OP/PA < OP/PC

or, e₁ < e₂

i.e., e on the steeper line AB < e on the flatter line CD.

It can be now easily proved e₁ < e₂ also at any price other than OP. For example, at p = OP₁, i.e., at the point F₁, having

e on the line AB (= e₁) < e on the line CD₁

[^._.^. the line AB is steeper than the line CD₁ at the point F₁]

Again, e on the line CD₁ = e on the line CD (= e₂)

[^._.^. the vertical intercepts or p-intercepts of both these lines are equal (2.1.7(ii)]

Therefore, e₁ < e₂ at p = OP₁.

Therefore, if the two straight line demand curves in­tersect, then, of them, the steeper line would be less elas­tic and the flatter line would be more elastic. Obviously, these two lines would be non-iso-elastic.

Type # 5. Vertical and Horizontal Demand Curves:

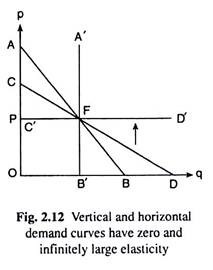
The more steep the steeper line, AB, in Fig. 2.11, the smaller would be e₁ at the point of intersection F of the two demand curves. In the limit, when the curve AB becomes the steepest, i.e., when the curve becomes a vertical straight line like A’B’ in Fig. 2.12, the value of e, would become the minimum, i.e., e₁ = 0 [e₁ (in the limit) = OP/PA = OP/∞ = 0 (^._.^. PA→∞)].

In fact, as seen that at each point on a verti­cal straight line demand curve, e = 0 (Fig. 2.3).

On the other hand, the flatter the line CD, in Fig. 2.11, the larger would be the value of e₂ at the point F. In the limit, when the curve CD becomes the flattest, i.e., when the curve becomes a horizontal straight line like C’D’ in Fig. 2.12, the value of e₂ would be the maximum, i.e., e₂ = ∞

(e₂ (in the limit) = OP/PC = OP/O = ∞ (^._.^. Pc →0)

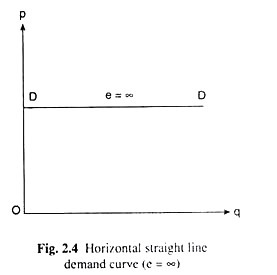
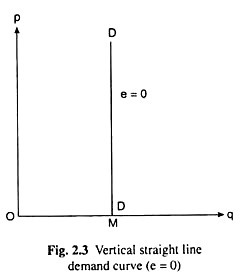
Of course, at each point on a horizontal straight line demand curve, e = ∞ (Fig. 2.4).

Type: 6. Uniformly Elastic Demand Curve:

It is clear, that the value of e is not the same at every point on a negatively sloped straight line demand curve—at some point(s), e = 1, at some other point(s), e > 1, at some other point(s) yet, e < 1. Therefore, such a demand curve has a segment of relatively elastic demand, a segment of relatively inelastic demand, and a segment of unitary elastic demand.

That is, it would be a mistake to assume that a steeper demand curve (line) would be relatively less elastic everywhere and a flatter demand curve (line) would be relatively more elastic always.

If the demand curve is a vertical or horizontal straight line, then at each point on such demand curves the value of e would be obtained to be the same. In the vertical case, e = 0 at each point and, in the horizontal case, everywhere  e = ∞

Like the negatively sloped straight line demand curves, in the case of curvilinear demand curve also, barring one exception, e at different points p would be different. On the same demand curve at some points e > 1, at some points, e = 1 and yet, at some other points, e < 1.

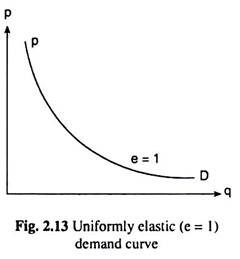
Only when the negatively sloped demand curve is a rectangular hyperbola like the curve DD in Fig. 2.13 that the value of e at every point on this curve would be the same, it would be equal to one (e = 1).

This is because at every point on such a de­mand curve, the total outlay of the buyers (p x q) would be the same, i.e., in this case, even if p changes, the buy­ers’ total expenditure on the good remains unchanged. Here, e would be equal to one. The point can be proved mathematically also. The equation of a rectangular hyperbola demand curve is

p x q = C (where C is a constant)

or p dq + q dp = 0 (taking total differential)

or dq/dp = –q/p

Therefore, at each point on this curve, it can be obtained: