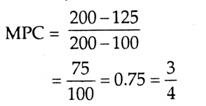Keynes Consumption Function (Attributes)

To construct macroeconomic models as devel­oped by Keynes, it is necessary to have a clear understanding of the consumption function.

In fact, the concept of the consumption func­tion is the ‘heart’ of the Keynesian analysis.

The concept of propensity to consume (i.e., willingness to consume) or the so-called con­sumption function is based on a ‘fundamen­tal psychological law’ which states that ‘men are disposed, as a rule and on the average, to increase their consumption as their income increases, but not by as much as the increase in their income’.

Although many factors in­fluence aggregate consumption, aggregate income or national income is, by far, the most important one in the Keynesian theory. So, here we will concentrate on the relationship between planned consumption and income the consumption function.

Keynes’ consumption function has the fol­lowing attributes:

1. Consumption is a stable function of income, i.e., C = f(Y).

2. Consumption is assumed to vary directly with income. As income rises, consump­tion rises.

3. The rate of increase in consumption is less than the rate of increase in income. In Keynes’ terminology, the value of the marginal propensity to consume (MPC) is less than one (i.e., MPC < 1).

4. MPC is less than the average propensity to consume (APC) in the short run (MPC < APC).

Here, consumption expenditure is a planned one, but not the actual one. Thus, in a consumption function, a relationship between national income and planned consumption expenditure is established.

Before elaborating on Keynes’ consump­tion function, let us explain the terminologies of APC and MPC.

1. APC and MPC:

APC is the ratio of consumption to income. It is the proportion of income that is consumed. It is worked out by dividing total consumption expenditure (C) by total income (Y). Symbolically,

APC = C/Y

MPC measures the response of con­sumption spending to a change in income. It is the ratio of change in consumption to a change in income. It is worked out by dividing the change in consumption by the change in income. Symbolically,

MPC = ∆C/∆Y

Suppose, national income rises from Rs. 100 crore to Rs. 200 crore. As a result, consumption spending rises from Rs. 125 crore to Rs. 200 crore. Thus,

In this example, MPC = 3/4 The economic meaning is that if national income rises by four rupees, consumption spending would increase by three rupees and the remainder one rupee would be saved. Notice that, in this example, the value of MPC is positive but less than one (0 > MPC < 1). Since at zero level of income consumption is positive, MPC must always be positive. Further, since increase in consumption is less than that of increase in income, the value of MPC must be less than one.

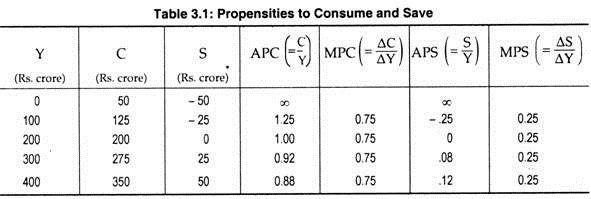
The relationship between planned consumption expenditure and income is presented in Table 3.1 in terms of a hypothetical data.

Table 3.1 tells us that when income is zero, consumption is positive (Rs. 50 crore). But as income increases, consumption rises. Further, as the rise in consumption is less than the rise in income APC declines. However, since the rate of increase in consumption is less than the rate of increase in income the value of MPC is always less than one (here 0.75). At the same time, MPC is always positive because consumption is positive even if income is zero. Finally, the table suggests that MPC < APC.

2. Consumption Function Equation:

The relationship between consumption spending and income is usually explained in an equation form:

C = a + bY (a > 0; 0 < b < 1)

Here, C and Y represent consumption and income, respectively. This equation indicates that consumption is a linear function of income since it is the equation of a straight line. In the equation, ‘a’ stands for autonomous consumption. This part of consumption spending is independent of the level of income.

Its value is positive in the sense that consumption is always positive, even if income is zero, ‘b’ is-the behavioural coefficient or the MPC. This part of consumption is called ‘induced’ consumption. According to Keynes, MPC is always positive, but less than one. Here ‘b’ is the slope of the consumption function. Thus, MPC is the slope of the consumption line.

1. Consumption Function in Graphical Form:

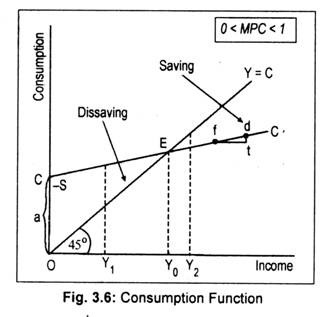
The consumption function equation can be represented in terms of Fig. 3.6 where we measure income on the horizontal axis and planned consumption expenditure on the ver­tical axis. All points on the 45° line show that the values measured on the two axes are equal (i.e., Y = C). The line CC’ is the consumption line which cuts the vertical axis at some posi­tive point. Positive vertical intercept (a > 0) of the consumption function implies that planned consumption expenditure exceeds income at very low levels of income. The line CC’ is upward rising.

This means—as income rises, consumption rises. Such consumption is called induced consumption. At an income level of OY₀, CC’ line coincides with the 45° line. That is to say, at point E income equals consumption. Such equality of income and consumption is called breakeven point. To the left of point E, say at OY₁ income level, as con­sumption exceeds income there occurs nega­tive saving or dissaving. This means that peo­ple consume more than their income, i.e., they spend their past savings. Actually, to the left of point E, CC’ line lies above the 45° line and to determine dissaving we have used -S sign in Fig. 3.6. On the other hand, to the right of E, i.e., at an income level of OY₂, income ex­ceeds consumption (and, hence, CC’ line lies below the 45° line) and positive saving occurs. As people do not spend their entire income on consumption, the rest is saved.

One can determine APC and MPC from the position or the location of CC’ line and slope of the CC’ line, respectively. At zero in­come, APC = . As income rises, APC declines but it never becomes zero. To determine the value of MPC, we have chosen two points f and d on the line CC’. As we move from f to d, income rises (Δ Y) by ‘ft’ and consumption rises (AC) by ‘dt’. Thus, MPC= ∆C/∆Y = dt/ft = slope of the line CC’. Its value is less than unity since the rate of increase in consump­tion (dt) is less than the rate of increase in income (ft). As CC’ is a straight line, MPC re­mains constant at all levels of income.

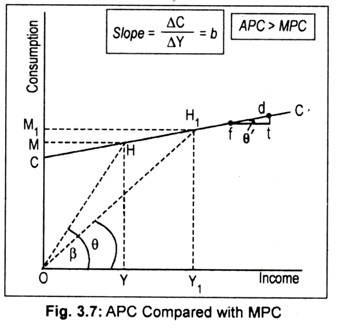
Though MPC remains constant as income rises, APC continuously declines on a straight line consumption function. This may be explained by examining Fig. 3.7. Let us consider point H on the line CC’. Correspon­ding to this point, income is OY and consumption is OM.

Thus, APC at point H is given by:

APC= OM/OY

Now consider the dashed lines β and θ drawn from the origin. Lines such as these are called rays. The slope of the ray P is equal to the tangent of the angle β and is, therefore, equal OM/OY to Thus, the slope of the ray to point H is the APC at point H. Similarly, the slope of the ray to point H₁ is the APC. In other words, the slope of the dashed lines OH and OH₁represent APCs at points H and H_p respectively. Since the slope of the ray OH₁ is less steep than that of the slope of the ray OH, APC declines as income rises.

To calculate MPC, one must take into account the slope of the consumption line CC’ between points, such as f and d, in Fig. 3.7. By inspection, we can see that tan β or tan θ is greater than tan θ’. This suggests that APC > MPC. So, we can conclude that the coordinates at any point on a consumption line give us the value of APC and the slope between any two points gives us the value of MPC.

Consider Fig. 3.6 again. At zero income APC = ; to the left of point E, APC > 1; at point E, APC = 1; and to the right of point E, APC < 1. On the other hand, 0 < MPC < 1. On a straight line consumption function, MPC remains constant at all levels of income. Thus, the Keynesian consumption function of the short run variety shows that APC > MPC.

We can prove this in the following way.

The equation of the linear consumption line

Is C= a+ bY. From this equation, one obtains

APC = C/Y =a/Y + b,

and MPC = b.

Thus, APC > MPC by the amount.

Keynes’ consumption function is a short run one and the relationship between consumption and income is a non-proportional one in the sense that MPC < APC.

However, a long run consumption function shows a proportional relationship between income and consumption. Because of this proportional relationship, MPC = APC. The long run consumption function starts from the origin. Its functional form is, thus, C = bY.