1. Absolute Income Hypothesis:
Keynes’ consumption function has come to be known as the ‘absolute income hypothesis’ or theory. His statement of the relationship between income and consumption was based on the ‘fundamental psychological law’.
He said that consumption is a stable function of current income (to be more specific, current disposable income—income after tax payment).
Because of the operation of the ‘psychological law’, his consumption function is such that 0 < MPC < 1 and MPC < APC. Thus, a non- proportional relationship (i.e., APC > MPC) between consumption and income exists in the Keynesian absolute income hypothesis. His consumption function may be rewritten here with the form
C = a + bY, where a > 0 and 0 < b < 1.
ADVERTISEMENTS:
It may be added that all the characteristics of Keynes’ consumption function are based not on any empirical observation, but on ‘fundamental psychological law’, i.e., experience and intuition.
(i) Consumption Function in the Light of Empirical Observations:
Meanwhile, attempts were made by the empirically-oriented economists in the late 1930s and early 1940s for testing the conclusions made in the Keynesian consumption function.
(ii) Short Run Budget Data and Cyclical Data:
Let us consider first the budget studies data or cross-sectional data of a cross section of the population and then time-series data. The first set of evidence came from budget studies for the years 1935-36 and 1941-42. These budget studies seemed consistent with the Keynes’ own conclusion on consumption-income relationship. The time-series data of the USA for the years 1929-44 also gave reasonably good support to the Keynesian theoretical consumption function.
Since the time period covered is not long enough, this empirical consumption function derived from the time- series data for 1929-44 may be called ‘cyclical’ consumption function. Anyway, we may conclude now that these two sets of data that generated consumption function consistent with the Keynesian consumption equation, C = a + bY.
ADVERTISEMENTS:
Further, 0 < b < 1 and AMC < APC.
(iii) Long Run Time-Series Data:
However, Simon Kuznets (the 1971 Nobel prize winner in Economics) considered a long period covering 1869 to 1929. His data may be described as the long run or secular time-series data. This data indicated no long run change in consumption despite a very large increase in income during the said period. Thus, the long run historical data that generated long run or secular consumption function were inconsistent with the Keynesian consumption function.
From Kuznets’ data what is obtained is that:
(a) There is no autonomous consumption, i.e., ‘a’ term of the consumption function and
ADVERTISEMENTS:
(b) A proportional long run consumption function in which APC and MPC are not different. In other words, the long run consumption function equation is C = bY.
As a = 0, the long run consumption function is one in which APC does not change over time and MPC = APC at all levels of income as contrasted to the short run non-proportional (MPC < APC) consumption-income relationship. Being proportional, the long run consumption function starts form the origin while a non-proportional short run consumption function starts from point above the origin. Keynes, in fact, was concerned with the long run situation.
But what is baffling and puzzling to us that the empirical studies suggest two different consumption functions a non-proportional cross-section function and a proportional long run time-series function.
2. Relative Income Hypothesis:
Studies in consumption then were directed to resolve the apparent conflict and inconsistencies between Keynes’ absolute income hypothesis and observations made by Simon Kuznets. Former hypothesis says that in the short run MPC < APC, while Kuznets’ observations say that MPC = APC in the long run.
One of the earliest attempts to offer a resolution of the conflict between short run and long run consumption functions was the ‘relative income hypothesis’ (henceforth R1H) of ).S. Duesenberry in 1949. Duesenberry believed that the basic consumption function was long run and proportional. This means that average fraction of income consumed does not change in the long run, but there may be variation between consumption and income within short run cycles.
Duesenberry’s RIH is based on two hypotheseis first is the relative income hypothesis and second is the past peak income hypothesis.
Duesenberry’s first hypothesis says that consumption depends not on the ‘absolute’ level of income but on the ‘relative’ income— income relative to the income of the society in which an individual lives. It is the relative position in the income distribution among families influences consumption decisions of individuals.
A households consumption is determined by the income and expenditure pattern of his neighbours. There is a tendency on the part of the people to imitate or emulate the consumption standards maintained by their neighbours. Specifically, people with relatively low incomes attempt to ‘keep up with the Joneses’—they consume more and save less. This imitative or emulative nature of consumption has been described by Duesenberry as the “demonstration effect.”
The outcome of this hypothesis is that the individuals’ APC depends on his relative position in income distribution. Families with relatively high incomes experience lower APCs and families with relatively low incomes experience high APCs. If, on the other hand, income distribution is relatively constant (i.e., keeping each families relative position unchanged while incomes of all families rise). Duesenberry then argues that APC will not change.
ADVERTISEMENTS:
Thus, in the aggregate we get a proportional relationship between aggregate income and aggregate consumption. Note MPC = APC. Hence the R1H says that there is no apparent conflict between the results of cross-sectional budget studies and the long run aggregate time-series data.
In terms of the second hypothesis short run cyclical behaviour of the Duesenberry’s aggregate consumption function can be explained. Duesenberry hypothesised that the present consumption of the families is influenced not just by current incomes but also by the levels of past peak incomes, i.e., C = f(Yri, Ypi), where Yri is the relative income and Ypi is the peak income.
This hypothesis says that consumption spending of families is largely motivated by the habitual behavioural pattern. It current incomes rise, households tend to consume more but slowly. This is because of the relatively low habitual consumption patterns and people adjust their consumption standards established by the previous peak income slowly to their present rising income levels.
On other hand, if current incomes decline these households do not immediately reduce their consumption as they find if difficult to reduce their consumption established by the previous peak income. Thus, during depression consumption rises as a fraction of income and during prosperity consumption does increase slowly as a fraction of income. This hypothesis thus generates a non-proportional consumption function.
ADVERTISEMENTS:
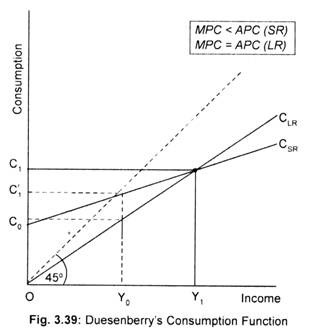
Duesenberry’s explanation of short run and long run consumption function and then, finally, reconciliation between these two types of consumption function can now be demonstrated in terms of Fig. 3.39. Cyclical rise and fall in income levels produce a non-proportional consumption-income relationship, labelled as CSR. In the long run as such fluctuations of income levels are get smoothened, one gets a proportional consumption-income relationship, labelled as CLR.
As national income rises consumption grows along the long run consumption, CLR. Note that at income OY0 aggregate consumption is OC0. As income increases to OY1, consumption rises to OC1. This means a constant APC consequent upon a steady growth of national income.
Now, let us assume that recession occurs leading to a fall in income level to OY0 from the previously attained peak income of OY1. Duesenberry’s second hypothesis now comes into operation: households will maintain the previous consumption level what they enjoyed at the past peak income level. That means, they hesitate in reducing their consumption standards along the CLR. Consumption will not decline to OC0, but to OC’1 (> OC0) at income OY0. At this income level, APC will be higher than what it was at OY1 and the MPC will be lower.
ADVERTISEMENTS:
If income rises consequent upon economic recovery, consumption rises along CSR since people try to maintain their habitual or accustomed consumption standards influenced by previous peak income. Once OY1 level of income is reached consumption would then move along CLR. Thus, the short run consumption is subject to what Duesenberry called ‘the ratchet effect’. It ratchets up following an increase in income levels, but it does not fall back downward in response to income declines.
3. Permanent Income Hypothesis:
Another attempt to reconcile three sets of apparently contradictory data (cross-sectional data or budget studies data, cyclical or short run time-series data and Kuznets’ long run time-series data) was made by Nobel prize winning Economist, Milton Friedman in 1957. Like Duesenberry’s RIH, Friedman’s hypothesis holds that the basic relationship between consumption and income is proportional.
But consumption, according to Friedman, depends neither on ‘absolute’ income, nor on ‘relative’ income but on ‘permanent’ income, based on expected future income. Thus, he finds a relationship between consumption and permanent income. His hypothesis is then described as the ‘permanent income hypothesis’ (henceforth PIH). In PIH, the relationship between permanent consumption and permanent income is shown.
Friedman divides the current measured income (i.e., income actually received) into two: permanent income (Yp) and transitory income (Yt). Thus, Y = Yp + Yt. Permanent income may be regarded as ‘the mean income’, determined by the expected or anticipated income to be received over a long period of time. On the other hand, transitory income consists of unexpected or unanticipated or windfall rise or fall in income (e.g., income received from lottery or race). Similarly, he distinguishes between permanent consumption (Cp) and transistory consumption (Ct). Transistory consumption may be regarded as the unanticipated spending (e.g., unexpected illness). Thus, measured consumption is the sum of permanent and transitory components of consumption. That is, C = Cp + Ct.
Friedman’s basic argument is that permanent consumption depends on permanent income. The basic relationship of PIH is that permanent consumption is proportional to permanent income that exhibits a fairly constant APC. That is, C = kYp where k is constant and equal to APC and MPC.
While reaching the above conclusion, Friedman assumes that there is no correlation between Yp and Yt, between Yt and Ct and between Cp and Ct. That is
ADVERTISEMENTS:
RYt. Yp = RYt . Ct = RCt. Cp = 0.
Since Yt is uncorrected with Yp, it then follows that a high (or low) permanent income is not correlated with a high (or low) transitory income. For the entire group of households from all income groups transitory incomes (both positive and negative) would cancel each over out so that average transitory income would be equal to zero. This is also true for transitory components of consumption. Thus, for all the families taken together the average transitory income and average transitory consumption are zero, that is,
Yt = Ct = 0 where Y and C are the average values. Now it follows that
Y = Yp and C = Cp
Let us consider some families, rather than the average of all families, with above-average measured incomes. This happens because these families had enjoyed unexpected incomes thereby making transitory incomes positive and Yp < Y. Similarly, for a sample of families with below-average measured in come, transitory incomes become negative and Yp > Y.
Now, we are in a position to resolve the apparent conflict between the cross-section and the long run time-series data to show a stable permanent relationship between permanent consumption and permanent income.
ADVERTISEMENTS:
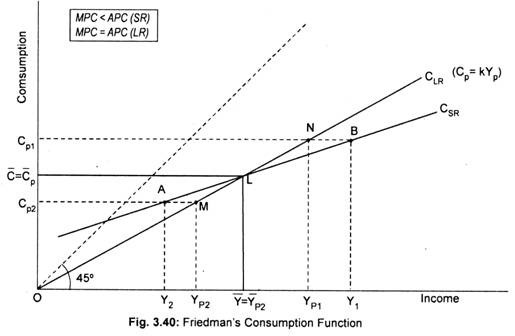
The line Cp = kYp in Fig 3.40 shows the proportional relationship between permanent consumption and permanent income. This line cuts the CSR line at point L that corresponds to the average measured income of the population at which Yt = 0. This average measured income produces average measured and permanent consumption, Cp.
Let us first consider a sample group of population having an average income above the population average. For this population group, transistory income is positive. The horizontal difference between the short run and long run consumption functions (points N and B and points M and A) describes the transitory income. Measured income equals permanent income at that point at which these two consumption functions intersect, i.e., point L in the figure where transitory income in zero.
For a sample group with average income above the national average measured income (Y1) exceeds permanent income (YP1). At (CP1) level of consumption (i.e., point B) average measured income for this sample group exceeds permanent income, YP1. This group thus now has a positive average transitory income.
Next, we consider another sample group of population whose average measured income is less than the national average. For this sample group, transitory income component is negative. At Cp2 level of consumption (i.e., point A lying on the CSR) average measured income falls short of permanent income, Yp2. Now joining points A and B we obtain a cross- section consumption function, labelled as CSR. This consumption function gives an MPC that has a value less than long run proportional consumption function, Cp = kYp. Thus, in the short run, Friedman’s hypothesis yields a consumption function similar to the Keynesian one, that is, MPC < APC.
However, over time as the economy grows transitory components reduce to zero for the society as a whole. So the measured consumption and measured income values are permanent consumption and permanent income. By joining points M, L and N we obtain a long run proportional consumption function that relates permanent consumption with the permanent income. On this line, APC is fairly constant, that is, APC = MPC.