We know that a tax increase results in a decline in income. In other words, it is contractionary in effect. An increase in tax (∆T) leads to a decrease in income (∆Y). The ratio of ∆Y/∆T, called the tax multiplier, is designated by KT Thus,
KT = ∆Y/∆T, and ∆Y = KT. ∆T
Again, how much national income would decline following an increase in tax receipt depends on the value of MPC. The formula for KT is
Thus, tax multiplier is negative and, in absolute terms, one less than government spending multiplier. If MPC = 3/4 then the value of KT = (-3/4)/(1-3/4)= -3.an increase in taxes of Rs. 20 crore results in a decline of income of Rs. 60 crore. That is to
ADVERTISEMENTS:
-60 = (-3/4)/(1-3/4)
In contrast, with an MPC = 3/4, the value of KG = 4. Assume an increase in government expenditure of Rs. 20 crore. Applying the formula for KG, we obtain
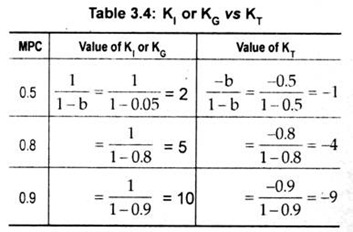
Thus, KT is negative and its value is one short of K, or KG.
ADVERTISEMENTS:
Graphically, tax multiplier has been shown in Fig. 3.18. Pre-tax consumption line and aggregate demand schedule are represented by C1 and C, + I + G, respectively. The corresponding equilibrium level of income is OYI. An increase in taxes shifts the consumption line to C2. Consequently, aggregate demand schedule also shifts downwards to C, + I + G. Consequently, income declines to OY2. Thus, the effect of an increase in taxes on income is contractionary.
One must know the distinction between KI or KG and KT.This is demonstrated in terms to Table 3.4.
Thus, KT is negative and one less than KI or KG.
The G-multiplier and T-multiplier are also called fiscal multipliers as these multipliers are associated with the fiscal activities of the government (i.e., changes in expenditure and taxation plans).
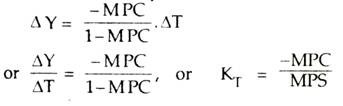
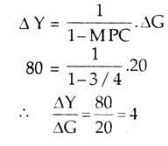
![clip_image002_thumb2[1] clip_image002_thumb2[1]](https://www.economicsdiscussion.net/wp-content/uploads/2015/04/clip_image002_thumb21_thumb1.jpg)