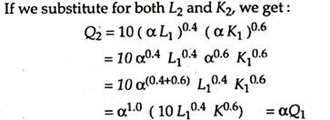In this article we will discuss about returns to scale. Also learn about the different and various types of returns to scale, explained with the help of a suitable graph.
The effect that the proportionate increase in all inputs has an output is a question of returns to scale. A firm changes its scale when it increases all of its inputs in the same (fixed) proportion.
Different types of Returns to Scale:
Average output per unit of inputs can do one of three things: increase, decrease or stay constant (i.e., remain the same). For example, if by doubling inputs, the firm doubles its output rate, it experiences constant returns to scale. If output were more than doubled as inputs doubled, there would be increasing returns to scale. If output were to less than double, there would be decreasing returns to scale.
ADVERTISEMENTS:
Determination of Scale of Economies:
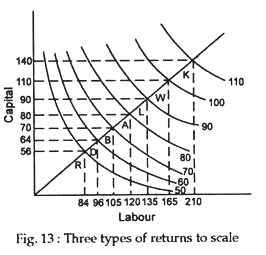
Fig. 13 shows the effects of doubling of both the number of labourers and the number of machines from L1 and K to L2 and K2. Since both labourers and machines are twice as large as before, the two inputs -are in the same proportion.
In Fig. 13 doubling the inputs has resulted in more than a doubling of output from 28 to 60. This is an example of IRS. By doubling both inputs again to L3 and K3, the firm experiences an output rate of 100, which is less than twice the output rate of 60. This is an example of decreasing returns to scale over this input range.
Fig. 13 shows that returns to scale vary over the range of possible outputs of the firm.
(c) We can demonstrate the extent of scale of economies directly from one equation of the production function.
For example, assume that the production function is as follows:
Q = 10 L0.4 K0.6
By the definition of scale of economies, we must increase both L and K in the same proportion and observe whether output increases in the same proportion. Assume that we multiply both L and K by a constant, a. For example, let a equal 2. We will use the constant a to show the generality of the result.
ADVERTISEMENTS:
Assume that we start with L1 and K1 units of the inputs. These inputs produce Q1 units of the output; that is,
Q1 = 10L10.4 K0.6
Now, let us multiply the inputs by the constant, α, so that L2 equals αL1and K2 equals αK1.
We now have:
Q2 = 10L20.4 K0.6
Since Q2 equals a Q1, this production function exhibits constant return to scale. By multiplying the inputs by a, we increase output in the same proportion. This result depends critically on the exponents of the inputs in the production function. In case the two exponents, 0.4 and 0.6, added up to 1 the production function would show constant returns to scale.
If the sum of the exponents had been less than 1, there would have been decreasing return to scale (that is, output would have increased by less than a times the original output). If the sum of the exponents had been greater than 1, there would have been increasing return to scale.