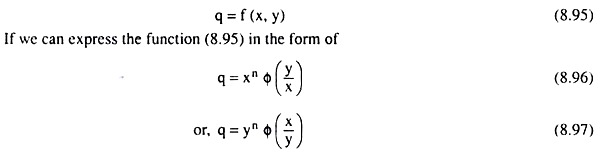Returns to Scale | Production

We may illustrate the returns to scale with the help of homogeneous production functions. Let us suppose that the production function of a firm is

 

 

 

 

 

 

then the function is called a homogeneous production function in x and y of degree n. One of the properties of a homogeneous function is that if (8.95) is a homogeneous function of degree n, then we would get

f(λx, λy) = λⁿf(x, y) = λⁿq                                     (8.98)

where λ is a positive real number.

That is, if both x and y are changed λ times, then q would change λⁿ times.

Now if the production function is homogeneous of degree 1, then (8.98) would give us

f(λx, λy) = λq                                                            (8.99)

i.e., if we change (increase or decrease) both input quantities λ times (λ ≠1) then the output quantity (q) would also change (increase or decrease) λ times. That is, in the case of homogeneous production function of degree 1, we would obtain the operation of the law of constant returns to scale.

Again, if n > 1 in (8.98), the law of increasing returns to scale would operate. For, here if x and y increase X times (λ > 1), q would increase more than λ times; for example if n = 2, then if x and y increase λ times, q would increase λ² times. It may be noted here that, under increasing returns to scale, if x and y decrease (λ < 1) by a certain proportion, then output would decrease by a larger proportion.

Lastly, if n < 1 in (8.98), for example, if n = 1/2, then q would increase λ^1/2 times when x and y increase λ times (λ > 1). That is, if x and y increase by a certain proportion, then q would increase by a smaller proportion. In this case, we would get the law of decreasing returns to scale.

It should be noted here that, under decreasing returns to scale, if x and y decrease (λ < 1) then as x and y decrease by a certain proportion, q would decrease by a smaller proportion.