Keynes and Classicists: An Comparison

Read this article to learn about Keynes and Classicists: An Comparison !

The comparison between the Classical and the Keynesian model might be simple and clear if we write the equations of the models side by side.

We write the equations of the simple classical model and the complete Keynesian model below:

Thus, saving and investment equality give us equilibrium condition in both the systems.

We have seven equations and seven unknowns in both the models. The system is determinate in both the models. As it can be seen, the classical model differs from the Keynesian model in three respects. The difference is in the labour supply functions in equations (3) and (III). The second difference is in the money demand function in equations (4) and (IV). Lastly, there is a difference in the saving function in equations (5) and (V).

In the classical model the supply of labour is assumed to be a function of real wage rate and the money wage rate is assumed to be flexible in both directions. On the other hand, in the Keynesian model the supply of labour is assumed to be a function of the money wage rate which is inflexible at least in downward direction. The money wage cannot fall below W₀.

In the classical Model money demand is assumed to be a function of the level of income only. They considered only the transactions — precautionary demand for money — money is considered to be a function of medium of exchange only. However, in the Keynesian Model, money demand is assumed to be a function of both the level of income — medium of exchange of money — and the rate of interest — store of value function of money.

The speculative demand for money is Keynesian innovation. Lastly, Keynes assumed that income is the main determinant of saving and not the interest rate as the classicists assumed.

The conclusions are also different in the two models. In the classical model, full-employment equilibrium is automatically reached. But in the Keynesian model there is no such automatic mechanism. The equilibrium may be one of full-employment or underemployment. While the classical economists denied the possibility of underemployment equilibrium, Keynes argued that there is no difficulty of getting an underemployment equilibrium.

The “Classical Economists” maintained two propositions about the equilibrium properties of an economy — flexible wages and prices. First, that the equilibrium is one with full employment of labour. Second, that the nominal quantity of money in the economy only determines the equilibrium price level, but has no effect on the equilibrium value of any real variable.

A real variable is one which has an effect on the allocation of resources over time or at a point of time. For example, the relative prices of commodities affect the quantities of commodities produced and consumed at a point in time; the interest rate affects the quantities of commodities consumed over time.

In the present context, real variables are real income, the interest rate and the real wage rate. According to the second proposition, none of these variables are determined by the nominal quantity of money. Their equilibrium values depend on the real factors — technology, tastes and the quantity of resources in the economy.

In the classical model, money is neutral. An increase in the supply of money affects only the price level and the money wage rate, keeping the real variables unaffected. But, in the Keynesian model, money is not neutral. A change in the quantity of money affects both the real and monetary variables.

Let us now examine which is the crucial difference between the classical model and the Keynesian model. Some economists think that it is difference in the labour supply function, others think that it is the difference in the money demand function, others say it is the difference in the saving function, while still others say that it is none of these but something else which is implicit in the formal structure. The crucial difference in conclusion is the possibility of underemployment equilibrium in the Keynesian model and full employment in the classical model.

We want to see which differences cause underemployment equilibrium. Let us introduce in the classical model the Keynesian money demand function.

The classical model will look like the following:

(1) Y = f (N, K₀) (2) P. dY/dN = w (3) N = N (W/P)

Now (4) M₀ = kPY + L(r) (5) S = S(r) (6) I = I(r) and (7) S = I

Here we will obtain automatic full-employment from equations (1) to (3). Equations (5)to (7) will determine the interest rate and the equation (4) will determine the price level. The resulting model would have classical char­acter and full employment would be automatically achieved due to the as­sumption of wage-price flexibility. Thus, the addition of the speculative demand for money into the classical model will not generate underemployment equilibrium and, hence, it is not a crucial difference.

Similarly, we can see that the saving function will not make crucial difference either. If we replace the classical saving function by the Keynesian saving function.

The resulting model will have the following system of equations:

(1) Y = f(N, K₀) (2) dY/dN = (W/P) (3) N = N(W/P)

(4) M₀ = kPY (5) S = S(Y) (6) I = I(r) (7) S = I

In this case also, full employment will be automatically achieved from equations (1) to (3). The difference here is that a shift of the production function or a shift of the labour supply function will affect the interest rate which will change income and saving relative to investment. Hence the difference in the saving function is not a crucial difference between the models.

Instead of changing the money demand function and saving function separately, we change them at the same time. Here also full employment is automatically achieved because of wage-price flexibility. This model is also classical in character because, like the classical model, full employment is automatically achieved in the labour market, the rate of interest is determined from saving and investment functions and the money market determines the price level. Thus, it is seen that the difference in the saving and money demand functions together cannot explain the difference in conclusion.

From the above analysis, it is clear that the crucial difference between the classical and Keynesian money models is the labour supply function i.e. the equation three. If we replace equation(3) of the classical (labour supply function) model by the equation (iii) of the Keynesian model — keeping other equations unchanged — then automatic achievement of full employment will be prevented.

Thus, we can say that the assumption of inflexibility of wages — especially in the downward direction — is the crucial difference between the Keynesian and the classical model. Underemployment equilibrium in the Keynesian model is caused by the assumption of wage rigidity – which is the crucial assumption of Keynes. In fact, it was the only possible cause of unemployment.

We have seen in the previous analysis that wage flexibility results in full-employment equilibrium in the labour market and price flexibility results- in full-employment equilibrium in the output market. It is also true, in this model, that the nominal quantity of money cannot affect the interest rate. All real variables in the economy are also determined by tastes, technology and the quantity of resources.

The nominal quantity of money determines the price level To understand the debate concerning the two classical propositions, it is necessary to understand how price flexibility results in full employment equilibrium and what role the nominal quantity of money plays in the process. The crucial assumption in the model is not price flexibility, as such, but interest- rate flexibility. With a given quantity of nominal money, price flexibility is the means by which the interest rate changes to its equilibrium value.

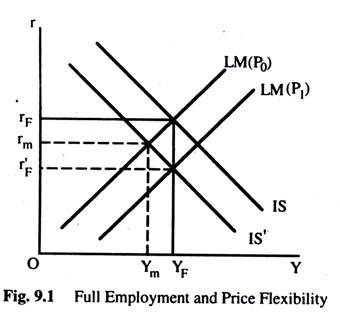
In Fig; 9.1, we start from full employment equilibrium of Y_Fr_F for some price level P₀. r_F is the interest rate at which full employment saving is equal to investment. Now, suppose that everybody wants to save more than previously — which shifts the IS curve to IS’. The new equilibrium interest rate is r_F at which new equilibrium saving is equal to investment at full employment. If there is no change in the price level, the interest rate will be r_m and the aggregate demand will be Y_m, less than, full employment output Y_F.

To attain full employment equilibrium again, the interest rate must fall and investment must rise. The reason is not far to seek. People wish to save more than before; they desire more future consumption relative to current consumption. So investment must increase. A change in the interest rate is the signalling device transmitting information about the change in tastes and producing the incentive to increase investment on this information.

However, this direct effect of the change in saving is on the price level and also on interest rate. With a given nominal quantity of money the tall in the price level leads to an increase in the real quantity of money and, thus, a fall in the interest rate.

As long as there is an excess of saving over investment and an excess supply of goods, the price level and, thus, interest rate, will continue falling If the interest rate reaches r_F with the price level P₁, full employment saving will equal investment again. Therefore, what is crucial to the first classical proposition is the interest rate flexibility without which price flexibility will not be enough to attain full employment.

In the above model, the second classical proposition also holds. A change in the nominal quantity of money, without any change in real factor, will affect price level only. Any initial effect on the interest rate will be offset by the change in the price level.

Keynes’ argument against the classical proposition is that it requires the interest rate flexibility which is the essential link between saving decisions and investment decisions. Now the question is whether price and wage flexibility guarantee the necessary interest rate flexibility? Keynes argued that in a money economy there is inherent inflexibility in the interest rate because the interest rate in such an economy could never fall below zero (the liquidity trap situation).

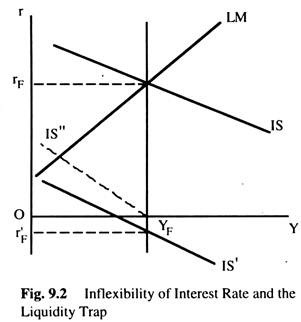
In Fig. 9.2, we start with a full-employment equilibrium at Y_F and r_F. Assume now that because of a change in tastes people want to save more at every level of income, shown by the shift of the IS curve to IS’. The equilibrium interest rate now is r_F at which full-employment saving is equal to investment which is negative and is an unacceptable rate in a money economy.

Thus, in Fig. 9.2, there is an excess of full-employment saving over investment, which will lead to a fall in the price level, but will not result in a-fall in the interest rate to the required level. Flexibility of prices does not imply the necessary flexibility of the interest rate as we can have the liquidity trap at a positive or zero rate of interest.

Here comes Pigou who criticises Keynes on this point which is known as ‘Pigou effect’ in the economic literature. He gave a solution to the problem raised by Keynes. Let us first look at the mechanism of the solution.

Any discrepancy between full-employment saving and investment can be eliminated either by a change in investment or in saving. Price flexibility can achieve a change in investment by a correct amount as long as it can affect a change in interest rate by a correct amount. Keynes’ point is that there is likely to be a situation where price flexibility may not do the trick; the interest rate cannot fall by the required amount and, thus, investment cannot rise by the required amount. However, another way out may be a change in saving. Again, the question is whether price flexibility can do this?

If consumption is solely a function of income, then a fall in the price level has no effect on consumption and thus on saving. One has to rely on investment effects to solve the discrepancy between investment and saving. If, however, consumption also depends on wealth, then a change in price can eliminate the discrepancy between saving and investment by affecting saving.

There exists a category of wealth which is affected by a change in the price level, namely the real quantity of money. For a given quantity of nominal money, the fall in the price level raises the real quantity of money and, thus, the perceived wealth of the community. Thus, the new function can be written as c = F (Y, M/P) a fall in the price level even if it has no effect on the interest rate (the Keynesian case) will still be effective in achieving full-employment by increasing consumption (reducing saving) and not by increasing investment (via a change in the interest rate). In Fig. 9.2, the change in the price level will shift the IS curve to IS”.

In the Keynesian case, we have a situation in which people want to save even at a zero rate of interest; they are not saving for the purpose of acquiring future income streams. They are then saving for the purpose of acquiring wealth for its own sake (positive time preference). They are willing to give up current consumption for the sake of accumulating wealth and, therefore, must be deriving some amenity value from it.

The Keynesian case can only arise if wealth is in the consumption function and we also have — via the “Pigou effect”— a solution to the Keynesian problem. The ‘Pigou effect’ is based on the idea that changes in the real quantity of money will affect consumption. A change in the real quantity of money may be achieved either by a change in the price level for a given quantity of nominal money or a change in the nominal quantity of money for a given price level. ‘Pigou Effect’ will be discussed in detail here.

Pigou Effect and Full-Employment:

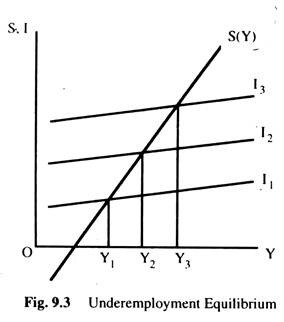
The basic difference between the Classical and the Keynesian economics is that, in the Classical Model, full-employment is automatically achieved, whereas, in the Keynesian model, no such automatic mechanism exists. In the simple Keynesian model of income determination, the equilibrium level of income is determined by the equality of planned saving and investment; the equilibrium level of income thus determined may or may not be full- employment equilibrium as given in Fig. 9.3.

If investment is I₁, the equilibrium level of income is Y₁. If investment is I₂, the equilibrium level of income is Y₂ and so on. Suppose the full employment level of income is Y₂ as determined from the labour market. The full-employment will be achieved only if the investment schedule is I₂. There is no reason to believe that the investment schedule will always be at I₂. Thus, there is no automatic machinery to ensure full employment.

Against the Keynesian argument the classical economists argue that saving and investment are functions of both the rate of interest and the level of income:

S = S(r, Y) and I = I(r, Y).

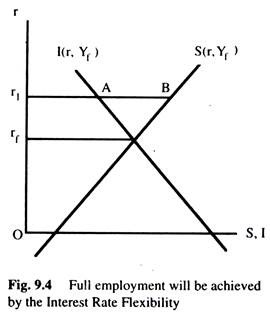
According to them, if saving at full employment is not equal to investment, the rate of interest will change and the flexibility of the interest rate will ensure the equality between investment and saving at full employment. We can see this in Fig. 9.4.

Suppose that investment and saving schedules are at full employment level of income. If the rate of interest is r₁, investment at full employment will be less than saving at full employment by the amount AB. Assuming that the rate of interest is flexible, the rate of interest will fall until saving becomes equal to investment at full employment. It is through flexibility of the interest rate that full employment is automatically achieved.

If the investment function is I₁, then saving at full employment will exceed investment. As a consequence the interest rate will fall. As the interest rate falls, the investment function shifts upwards until I₂ is reached. Thus, even if investment function is I₁ or I₃, it will eventually reach I₂ through the interest rate flexibility.

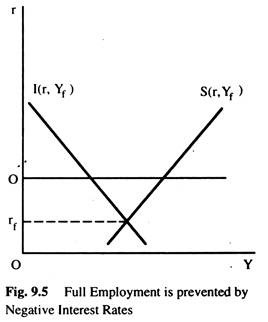
To this the Keynesian economists argue that, at times the saving and investment schedules are such that the rate of interest required to maintain full employment becomes zero or negative as shown in Fig 9.5. In Fig. 9.5, the saving and investment schedules intersect to produce a negative rate of interest at full employment.

In such a situation, full employ­ment cannot be achieved because a negative rate of interest is not feasible in a money economy. Whether the system will generate full employment depends on whether or not full employment saving and invest­ment intersect at a positive rate of interest.

However, there is no automatic mechanism to ensure that the investment and saving functions will always intersect at a positive rate of interest. Against this negative argument of Keynes, Pigou, Patinkin etc. have given replies. They introduced another variable into the saving function. The saving function can now be written as s = s{r, Y, M₀/P} where M₀/P is the real value of cash balances. They argue that as the real value of cash balances goes up (∂s/∂[M₀/P]), saving decreases.

The argument of Pigou is that if people save only to earn interest then saving would be, zero when the rate of interest is zero or negative. In that case, saving and investment would always intersect at a positive rate of interest. If people save even at a negative rate of interest, it means that they save for other reasons.

The extent of such saving out of current income is inversely related to the real value of cash balances. If this is sufficiently large, all the secondary desires for saving will be fulfilled. At this point, the only reason for saving is to earn future income. If the real value of cash balances is large enough, saving becomes zero at a positive rate of interest — irrespective of the income level.

The dependence of the saving function on the real value of the cash balances is known as Pigou Effect or Real Balance Effect. In short, Pigou Effect states that the aggregate consumption expenditure is directly related to the volume of wealth and saving is inversely related to the volume of wealth.

According to Pigou it is through the ‘Pigou Effect’ or the Real Balance Effect that full employment will be automatically achieved. The argument of negative rate is invalid, if we accept complete flexibility of prices. Suppose that at a given price level, the rate of interest needed to achieve full employment is negative.

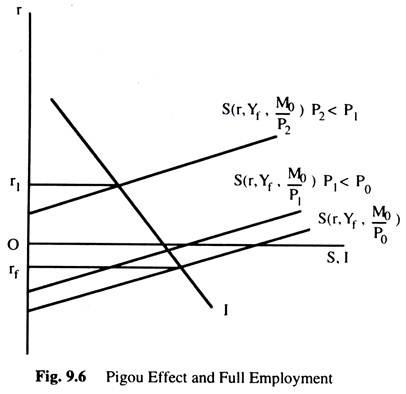
If full employment investment is less than saving, national income starts falling, and unemployment results. If workers accept the reduction of money wages then the price level will begin to fall which increases the real value of the given money supply. As a consequence, the saving function shifts to the left until it intersects the investment function at a positive rate of interest as shown in Fig. 9.6.

Assume that the initial price level is P₀, the investment function at full employment intersects the saving function at r_f, a negative rate of interest. As a result, the price level falls to P₁ and the real value of given money supply rises, i.e. M₀/P₁ > M₀/P₀. Thus, the saving function shifts to the left to a new position S[r, Y_f, M₀/P₁].

If the new saving function does not intersect the investment function at a positive rate of interest, the price level will fall further and the saving function will shift to the left until a positive rate of interest is achieved at full employment. Thus, the negative rate of interest will be avoided through the Pigou Effect. Thus, Pigou Effect ensures an automatic mechanism to full employment through the price flexibility.

The Pigou effect does not guarantee that full employment will always be achieved. Suppose that the strength of the Pigou effect is very small, so that a successive fall in the price level cannot produce a sufficient shift in the saving function to generate a positive interest rate. In such a situation the falling price level would fail to bring about full employment.

To achieve full employment we need an additional assumption, that the intensity of the Pigou effect is such that it would produce a sufficient shift in the saving function to intersect the investment function at a positive rate of interest.